1. Grundlagen
1.1 Grundlegende Begriffe
Die Stochastik beschäftigt sich allgemein mit dem Begriff der Wahrscheinlichkeit und der Statistik. Die Vorhersagen von Ereignissen werden dabei statistisch oder mit Hilfe von Experimenten untersucht, berechnet oder vorausgesagt. Beide Bereiche enthalten aber auch Problematiken.
- Traue keiner Statistik, die du nicht selber gefälscht hast. Oft werden die Untersuchungen falsch durchgeführt oder ausgewertet.
- Auch kann die Wahrscheinlichkeitsberechnung zu falschen Entscheidungen führen, da sich nicht alles zu 100% voraussagen lässt.
Bei der Statistik führt man Datenerhebungen innerhalb einer Gruppe durch. Dabei werden einzelne Merkmale der Gruppe betrachtet und auch miteinander kombiniert. Die Anzahl eines Merkmals wird in einer Liste aufgeschrieben und die absolute Häufigkeit damit festgestellt. Setzt man die absolute Häufigkeit mit der Gesamtanzahl ins Verhältnis, so berechnet man damit die relative Häufigkeit.
Relative Häufigkeit P(M)= absolute Häufigkeit / Größe der Gesamtmenge
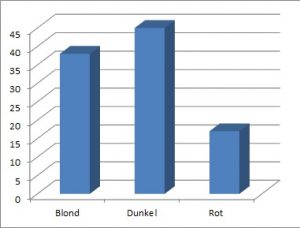
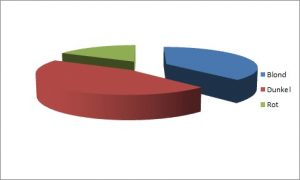
Beispiel: Von 100 Personen sind 38 blondhaarig, 45 dunkelhaarig und 17 rothaarig.
P(rot)=17/100
P(blond)=38/100
P(dunkel)=45/100
 |
 |
Bei der Wahrscheinlichkeitsrechnung untersucht man mit Zufallsexperimenten mögliche Ereignisse E und sagt damit Wahrscheinlichkeiten voraus. Alle möglichen Ereignisse eines Zufallsexperiments fassen wir in einer Ereignismenge Ω zusammen. Umfasst das Ereignis nur ein Element von Ω, dann handelt es sich um ein Elementarereignis.
Beispiel: Bei einem Würfel mit sechs Seiten wäre Ω={1, 2, 3, 4, 5, 6}. Ein mögliches Ereignis A ist, dass man eine gerade Zahl würfelt: A={2, 4, 6}. Ein Elementarereignis wäre B={6}, also das Ereignis, dass eine 6 gewürfelt wird.
Die Wahrscheinlichkeit eines Ereignisses E wird mit P(E) bezeichnet.
Beispiel: P(A) = 3/6 = 0,5 oder 50% und P(B) = 1/6 = 0,167 oder 16,7%
Manchmal ist es einfacher, das Gegenereignis Ē von einem Ereignis E zu betrachten, wenn dieses weniger Ausgänge hat. Da die Wahrscheinlichkeit für beides E und Ē 100% = 1 ergibt, kann man die Wahrscheinlichkeit für das Ereignis E mit folgender Regel für die Wahrscheinlichkeit des Gegenereignisses Ē berechnen. Also gilt:
P(Ē) = 1 – P(E) oder P(E) = 1 – P(Ē)
1.2 Laplace-Experiment
Häufig untersucht man solche Zufallsexperimente, bei denen jedes Elementarereignis die gleiche Wahrscheinlichkeit hat. Bei diesen Experimenten spricht man von Laplace-Experimenten.
Beispiele für Laplace-Experimente sind ein fairer Würfel oder eine Urne mit gleichgroßen Kugeln, das Werfen einer Münze oder das Ziehen einer Karte aus einem Kartenspiel. Hat die Ereignismenge n Elemente, so hat jedes Elementarereignis E dieselbe Wahrscheinlichkeit P(E) = 1/n.
Für ein Ereignis A gilt dann die Wahrscheinlichkeit: P(A) = |A|/n.
Dabei ist |A| die Anzahl möglicher Ausgänge für A und n ist die Anzahl aller möglichen Ausgänge.
Man kann auch mehrere Ereignisse untersuchen, das Ereignis A und das Ereignis B:
A∪B ist das Ereignis A oder Ereignis B (Vereinigungsmenge)
A∩B ist das Ereignis A und das Ereignis B (Schnittmenge)
Dann gilt für die Wahrscheinlichkeitsberechnung: P(A∪B) = P(A) + P(B) − P(A∩B)
Beispiel: In einer Urne sind 20 Kugeln mit den Ziffern von 1, 2, …, 20 beschriftet. Es wird zufällig eine Kugel gezogen. Wir betrachten folgende Ereignisse:
A: Es wird eine Kugel mit einer Ziffer gezogen, die durch 9 teilbar ist. A= {9, 18}, P(A) =2/20
B: Es wird eine Kugel mit einer Ziffer gezogen, die durch 6 teilbar ist. B= {6, 12, 18}, P(B) = 3/20
A∩B: Es wird eine Kugel gezogen, die durch 9 und 6 teilbar ist. A∩B= {18}, P(A∩B) = 1/20
A∪B: Es wird eine Kugel gezogen, die durch 9 oder 6 teilbar ist. A∪B = {6, 9, 12, 18}, P(A∪B) = 4/20
P(A∪B) = P(A) + P(B) − P(A∩B) = 2/20 + 3/20 – 1/20 = 4/20
1.3 Wahrscheinlichkeitsbaum
Komplizierte Zufallsexperimente, bei denen mehrmals gezogen wird oder mehrere Ereignisse betrachtet werden, kann man zur Vereinfachung in einem sogenannten Wahrscheinlichkeitsbaum aufzeichnen und die einzelnen Wahrscheinlichkeiten daran notieren. Dabei ist jede Stufe des Baums eine Ziehung oder ein anderes Merkmal. Dabei kann der Wahrscheinlichkeitsbaum waagerecht oder auch senkrecht aufgezeichnet werden.
Beispiel:
Zwei Ausgänge mit 3 Stufen:
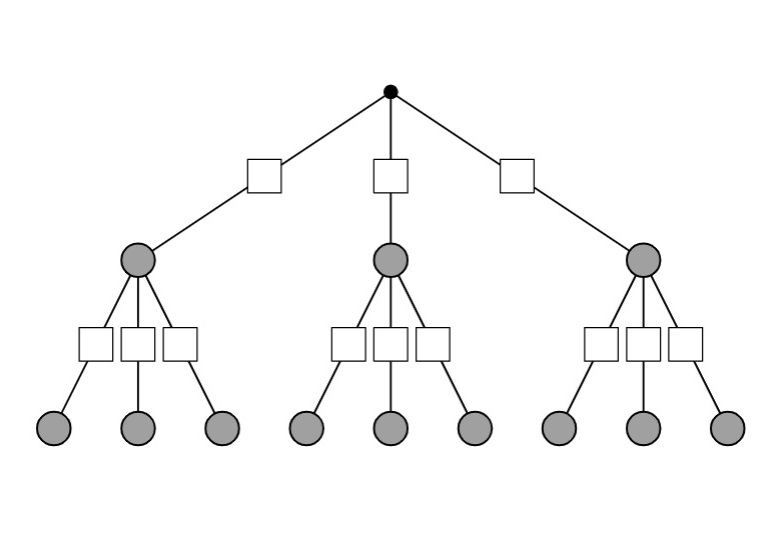
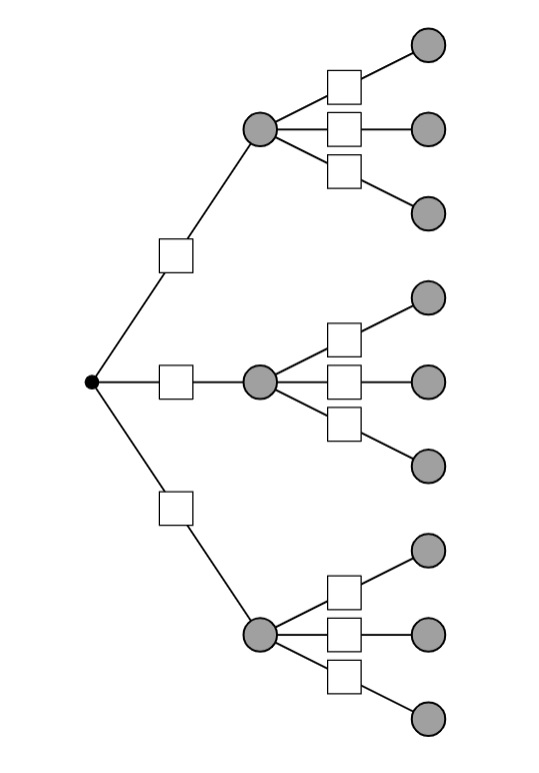
Drei Ausgänge mit 2 Stufen:
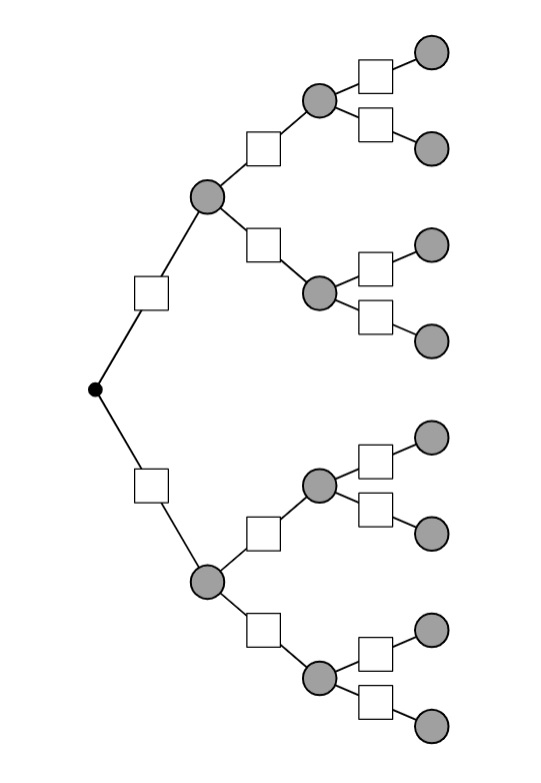
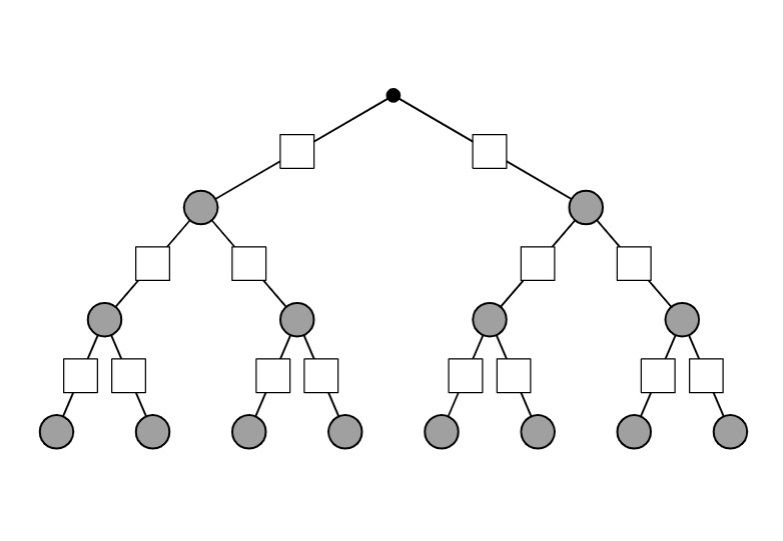
In die Kästen, d.h. an die Pfade werden die Wahrscheinlichkeiten dieses Ereignisses geschrieben. Am Ende eines Pfades steht dann die Wahrscheinlichkeit für diesen Pfad. Wie mit den Wahrscheinlichkeiten gerechnet wird, wird in der sogenannten Pfadregel beschrieben.
Pfadregel: Entlang eines Pfades werden die Wahrscheinlichkeiten multipliziert. Möchte man mehrere Pfade zusammen rechnen, so werden diese Wahrscheinlichkeiten addiert.
Beispiel: Eine Urne enthält 20 Kugeln mit drei verschiedenen Farben. 12 grüne (g), 5 rote (r) und 3 baue (b) Kugeln. Es wird 2-mal eine Kugel gezogen.
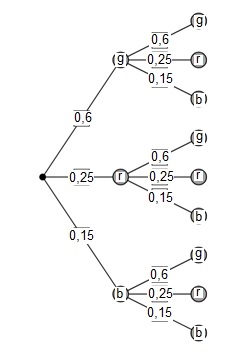
Wird die gezogene Kugel zurückgelegt, so ändert sich die Wahrscheinlichkeit bei den Ziehungen nicht
g = 0,6 = 60% r = 0,25 = 25% und b = 0,15 = 15%.
Die Wahrscheinlichkeit zweimal grün zu ziehen ist:
P((g,g)) = 0,6‧0,6 = 0,36 = 36%
Die Wahrscheinlichkeit zwei gleichfarbige Kugeln zu ziehen ist:
P((g,g))+P((r,r))+P((b,b)) = 0,6‧0,6+0,25‧0,25+0,15‧0,15
= 0,36+0,0625+0,025 = 0,4475 = 44,75%
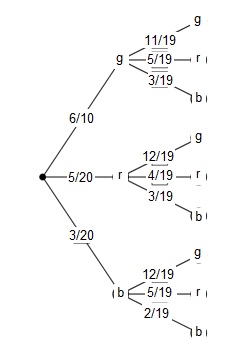
Wird die Kugel aber nicht zurückgelegt, so ändern sich die Wahrscheinlichkeiten, je nachdem welche Farbe bei der 1. Ziehung gezogen wird und es sind auch nur noch 19 Kugeln in der Urne.
Die Wahrscheinlichkeit zweimal grün zu ziehen ist:
P((g,g)) = 6/10‧11/19 = 0,6‧0,5789 = 0,3474 = 34,74%
Die Wahrscheinlichkeit zwei gleichfarbige Kugeln zu ziehen ist:
P((g,g))+P((r,r))+P((b,b)) = 6/10‧11/19+5/20‧4/19+3/20‧2/19
= 0,3474 +0,0526+0,0158 = 0,4158 = 41,58%
Beim mehrmaligen Würfeln mit einem Würfel kann man auch mit einem Baumdiagramm arbeiten.
Es wird 3-mal gewürfelt. Wie groß ist die Wahrscheinlichkeit dabei mindestens eine 6 zu würfeln?
Hierbei kann man das Baumdiagramm nur teilweise zeichnen, da man nur die Äste benötigt, wo eine sechs gewürfelt wird. Fällt die sechs, so braucht man die weiteren Ausgänge nicht mehr betrachten.

Die Wahrscheinlichkeit beträgt:
P(A) = 1/6 + 5/36 + 25/216 =0,4213 = 42,13%
Sobald im Baumdiagramm eine 6 vorkommt, kann der Ast beendet werden.
2. Möglichkeit mit dem Gegenereignis:
Das Gegenereignis Ā ist keine 6 zu würfeln.
P(A) =1−P(Ā) = 1− 125/216 = 1 -0,5787 ≈ 0,4213 = 42,13%