Die natürlichen Zahlen sind die Zahlen, die man beim Zählen verwendet. Die Menge der natürlichen Zahlen wird mit ℕ bezeichnet. ℕ={0, 1, 2, 3,4, …}.
Alle natürlichen Zahlen haben einen Nachfolger und bis auf die Null einen Vorgänger.
Der Nachfolger von 175 ist 176 und der Vorgänger von 188 ist 187.
Der Nachfolger von 1099 ist 1100 und der Vorgänger von 1200 ist 1199.
Die natürlichen Zahlen werden auf dem Zahlenstrahl in gleichen Abständen angeordnet.

Trägt man die Zahlen dort ein, so kann man sehen, welche Zahl größer oder kleiner ist. Ist eine Zahl weiter rechts auf dem Zahlenstrahl, so ist sie größer als die andere.
5 > 4, das heißt 5 ist „größer als“ 4 aber
5 < 6, das heißt 5 ist „kleiner als“ 6. Die Öffnung des Zeichens zeigt immer zur größeren Zahl.
- Große Zahlen – Stellenwerttafel
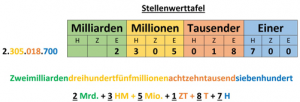
Bei der Bezeichnung von großen Zahlen werden immer 3 Stellen der Zahl zu einem Bereich zusammengefasst. Deshalb macht man bei den Zahlen auch häufig nach 3 Stellen einen kleinen Abstand. Nach dem Einer, Zehner und Hunderter-Bereich kommt der Tausender, dann die Millionen, Milliarden, Billionen, Billiarden, Trillionen, Trilliarden, Quadrillionen, Quadrilliarden, …. In einer Stellenwerttafel sieht dies so aus:
Die Zahl 67 320 455 321 lautet: 67 Milliarden 320 Millionen 455 Tausend 321 oder
Siebenundsechzigmilliardendreihundertzwanzigmillionenvierhundertfünfunffünfzigtausend-dreihunderteinundzwanzig.
- Zahlen runden
Bei vielen Angaben von Zahlen, wenn sie besonders groß sind, kommt es häufig nicht auf die genaue Zahl an, sondern man möchte nur eine ungefähre Zahl wissen. Deshalb werden große Zahlen häufig gerundet. Dabei gibt man immer an, auf welche Stelle die Zahl gerundet wird, z.B. auf Tausender oder Millionen. Ob nun diese Stelle aufgerundet wird (+1) oder abgerundet wird (sie bleibt), kommt auf die Stelle davor an. Steht hier eine Zahl zwischen 0 und 4 wird abgerundet (sie bleibt und alles davor wird zu Null) und ab 5 wird aufgerundet (+1 und alles davor wird zu Null).
Beispiel:
Runde auf Tausender : 51234 ≈51000 , da vor der Tausenderstelle (1) eine 2 steht und deshalb abgerundet wird.
Runde auf Millionen: 43 578 470 ≈44 000 000, da vor der Millionenstelle (3) eine 5 steht und deshalb aufgerundet wird. Die 3 wird zu 4 und alles vorher wird auf Null gesetzt.
- Zahlen schätzen – überschlagen
Damit man eine Anzahl abschätzen oder überschlagen kann, muss man sich eine Systematik überlegen. Ein Bild oder etwas, was man beobachtet, zerlegt man am Besten in gleich große Felder (Rechtecke oder Quadrate). Die Anzahl dieser Felder zählt man und man überschlägt oder zählt ein einzelnes Feld. Dann muss man für die Gesamtzahl diese beiden Werte nur noch multiplizieren. Manchmal könnte es auch einfacher sein, wenn man fehlende Positionen von der Gesamtzahl abzieht (bei einzelnen Lücken).

Beispiel 1:
Die Anzahl der Bäume sind 5*10=50 oder 4*10=40. Es kommt darauf an, welches Feld man abgezählt hat.

Beispiel 2:
Man hat ein Raster von 8 mal 6 Felder = 48 Felder
In einem Feld sind ca. 7 bis 8 Smarties zu sehen.
Insgesamt also 48 mal 7 = 336 oder 48 mal 8 =384 Smarties.
Aufgabenteil
1. Zeichne eine Stellenwerttafel bis Billionen und trage folgende Zahlen ein.
| a |
|
b |
|
||||||
| c |
|
d |
|
||||||
| e | 4 Billionen 76 Milliarden 34 Millionen 25 Tausend und 65 | f | 867 Milliarden 54 Millionen 276 Tausend und 8 |

2. Lies folgende Zahlen und schreibe in Worten.
| a | 7 600 23 000 156 343 100 |
b | 77 000 415 000 3 870 000 |
| c | 56 300 2 340 000 2 000 134 |
d | 800 340 23 900 000 52 900 500 |
| e | 4 000 244 000 | f | 54 230 390 200 |
3. Schreibe die Zahlen wie im Beispiel in Worten ohne Zahlen.
3 560 346 – dreimillionenfünfhundertsechzigtausenddreihundertsechsundvierzig
| a | 378 |
| b | 1 898 |
| c | 23 900 654 |
| d | 44 090 870 750 |
