5. Anwendungen der Ableitung
5.1. Kurvendiskussion
Zur Funktionsuntersuchung gehören vor allem folgende wesentliche Aspekte:
- Zur Funktionsuntersuchung benötigt man immer die ersten drei Ableitungsfunktionen.
- Man untersucht zuerst, wo die Funktion definiert ist (Definitionsbereich) und welche Funktionswerte erreicht werden(Wertebereich). Dies beinhaltet auch
- Das Verhalten der Funktion für x→±∞, evtl. asymptotisches Verhalten (Annäherung an eine Gerade oder Kurve)
- Das Verhalten der Funktion an den Definitionslücken, z.B. an Polstellen oder stetig behebbare Lücken.
- Man schaut nach einem Symmetrieverhalten, was bei Symmetrie die Berechnung von y-Werten erleichtern kann.
- Besondere Stellen und Punkte der Funktion werden berechnet:
y-Achsenschnittpunkt, Nullstellen, Extrempunkte, Wendepunkte - Aus allen Angaben wird dann ein Schaubild erstellt.
Definitionsbereich und Wertebereich:
Der Definitionsbereich sind die Werte von x, die man in die Funktion einsetzen darf. Entweder kann man dies aus dem Sachzusammenhang der Aufgabe erschließen, wenn z.B. nur positive oder nur natürliche Zahlen sinnvoll sind oder man darf nach den Rechenregeln bestimmte Zahlen nicht einsetzen. Zur Angabe des Definitionsbereichs kann man folgende Schreibweisen verwenden:
D = ℝ, alle reellen Zahlen sind erlaubt
D = ℚ, alle rationale Zahlen (als Bruch darstellbar) sind erlaubt
D = ℕ, alle natürlichen Zahlen sind erlaubt
D = ℤ, alle ganzen Zahle auch negative Zahlen sind erlaubt
D = ℝ/{0;1;2; ..}alle relle Zahlen außer 0, 1, 2 usw.
D = [-2;5], alle rellen Zahlen im Intervall von -2 bis 5
Der Wertebereich W = ℝ, sind alle Zahlen, die als y-Wert vorkommen kann. Manchmal kann man dies erst nach den besonderen Punkten entscheiden.
Grenzwertverhalten:
Wie verhält sich die Funktion im Unendlichen, d.h. für besonders große positiv und negative x-Werte? Hier untersucht man das Verhalten im Unendlichen durch sinnvolle Überlegungen.
lim f(x) = +∞ oder lim f(x) = – ∞
x→ +∞ x→ – ∞
Bei Polynomen ist dafür der Summand mit der größten Hochzahl verantwortlich, d.h. hier muss man nur den Teil mit dem höchsten Exponenten und dessen Vorzeichen betrachten.
Symmetrieverhalten:
Hier untersucht man zwei Symmetrien:
- eine Achsensymmetrie zur y-Achse, d.h. die Funktion ist an der y-Achse gespiegelt. Also ist hier f(x) = f(– x). Die y-Werte sind im negativen Bereich gleich den y-Werten im positiven Bereich.
- Eine Punktsymmetrie zum Koordinatenursprung, d.h. die Funktionswerte im negativen Bereich unterscheiden sich vom positiven Bereich nur durch das Vorzeichen.
Hier gilt: f(– x)= – f(x)
Bei Polynomen oder ganzrationalen Funktionen gilt folgende Regel:
- Achsensymmetrie zur y-Achse liegt vor, wenn nur gerade Hochzahlen vorkommen.
- Punktsymmetrie zum Ursprung liegt vor, wenn nur ungerade Hochzahlen vorkommen.
y-Achsenschnittpunkt:
Wo schneidet die Funktion die y-Achse? Da hier ja der x-Wert Null ist, muss man nur für x Null in f(x) einsetzen und erhält den Schnittpunkt mit der y-Achse.
y = f(0) →Sy(0|y)
Nullstellen:
Wo schneidet die Funktion f(x) die x-Achse? Hier kann es mehrere Stellen geben. Bei Polynomen oder ganzrationalen Funktionen ist die maximale Anzahl von Nullstellen gleich der höchste Exponent. Eine quadratische Funktion hat also maximal 2 Nullstellen, eine hoch 3 Funktion hat höchstens 3 Nullstellen usw.
Zur Berechnung muss man die Funktion gleich Null setzen und eine Gleichung lösen. Bei der Lösung der Gleichung gibt es verschiedene Lösungsverfahren wie Äquivalenzumformung, pq-Formel, Faktorisieren (Ausklammern), Polynomdivision oder Substitution bei biquadratischen Gleichungen.
a) Lineare Gleichungen
Man löst die Gleichung durch Umstellung der Gleichung nach x.
Beispiel: f(x) = 3x – 4
3x – 4 = 0 | +4
3x = 4 |:3
x = 4/3 ≈ 1,33→N(1,33|0)b) Quadratische Gleichung
b) Quadratische Gleichungen
Eine quadratische Gleichung kann man immer mit der pq-Formel lösen. Ist p oder q = 0, so kann man die Gleichung auch durch Ausklammern oder Wurzelziehen lösen.
Beispiele:
1) p-q-Formel
f(x) = 2x2 – 4x – 6
2x2 – 4x – 6 = 0 |:2
x2 – 2x –3 = 0 |p = – 2 ; q = –3; x1/2 = –p/2 ±√(p/2)2– q
x1/2 = 2/2 ±√(2/2)2+ 3
x1/2 = 1 ±√4=1±2
x1 = 3; x2= –1 →N1(3|0);N2(–1|0)
2) ausklammern
f(x) = 4x2 – 8x
4x2 – 8x = 0 | x ausklammern
x(4x – 8) = 0 | Satz vom Nullprodukt – Ein Produkt wird Null, wenn ein Faktor Null ist.
x = 0 ˅ 4x – 8 = 0 |+8 | :4
x = 0 ˅ x = 2 →N1(0|0); N2(2|0)
3) Wurzel ziehen
f(x) = 4x2 – 16
4x2 – 16 = 0 |+16 |:4
x2 = 4 |√
x = ±√4 = ±2 →N1(2|0); N2(–2|0)
c) Polynomdivision
Bei höheren Exponenten in der Gleichung kann man durch Suchen oder Erraten einer Lösung durch Division dann den Grad der Gleichung kleiner machen bis dann die Gleichung durch ein anderes Verfahren komplett lösbar wird. Man muss das Ausgangspolynom teilen durch das Polynom der gefundenen Nullstelle (x – x0).
Beispiel: f(x) = x3 – 6x + 5 = 0 Probiert man x1 = 1 aus, so erhält man beim Einsetzen Null. Dies ist also eine gefundene Nullstelle.
(x3 – 6x + 5):(x – 1) = x2 + x – 5
-(x3 – x2)
x2 – 6x + 5
-(x2 – x)
-5x + 5
-(-5x + 5)
0
Nun muss man nur noch das Ergebnis der Polynomdivision gleich Null setzen.
x2 + x – 5 = 0 | pq-Formel
x2/3 = -0,5 ±√0,25+5
x2/3 = -0,5 ±√5,25
x2 ≈ 1,79 ; x2 ≈ -2,79 →N1(1|0); N2(1.79|0); N3(-2,79)
d) Substitution
Hat man in der Gleichung nur Potenzen von x, die ein Vielfaches sind, so kann man diese Potenzen ersetzen durch z = xn. Beispiel: (z = x2 und z2 = x4 ) oder (z = x3 und z2 = x6 ) oder (z = x4 und z2 = x8). Nach der Substitution erhält man Lösungen für z, die man dann noch in die Substitution einsetzen muss, um Lösungen für x zu erhalten.
Beispiel: 2x4 – 4x2 – 6 = 0 |Substitution z=x2; z2=x4
2z2 – 4z – 6 = 0 |:2
z2 – 2z – 3 = 0 |pq-Formel
z1/2 = 1 ± √1+3
z1/2 = 1 ± 2
z1 = 3 ; z2 = -1
Lösungen für x: x2 = 3; x1=+√3 ; x2= -√3 →N1(√3|0); N2(-√3|0)
x2 = -1 hat keine Lösungen
Hoch- und Tiefpunkte:
Den x-Wert eines Hoch- bzw. Tiefpunkts bezeichnet man als Extremstelle, den dazugehörigen Funktionswert als Extremwert (=lokales Maximum oder Minimum).
An jedem Hochpunkt und an jedem Tiefpunkt hat f die Tangentensteigung 0 (obere beide Skizzen).
Tangentensteigung 0 bedeutet aber nicht automatisch, dass es sich
um einen Hoch- bzw. Tiefpunkt handelt.
Es könnte auch ein sogenannter Sattelpunkt (=Terrassenpunkt) sein (untere Skizze).
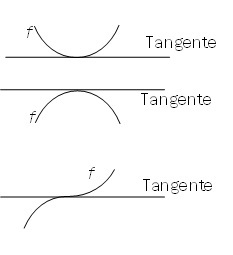
Somit formuliert man die
Notwendige Bedingung für Extremstellen x0 : f´(x0) = 0
Damit tatsächlich ein Hochpunkt vorliegt, muss die Steigung von f links der Extremstelle positiv
und rechts der Extremstelle negativ sein.
Mit anderen Worten: f´ hat an der Extremstelle einen Vorzeichenwechsel von + nach –.
Ebenso muss f´ bei einem Tiefpunkt einen Vorzeichenwechsel von – nach + haben.
Bei einem Sattelpunkt ist beides nicht der Fall, dort hat f´ keinen Vorzeichenwechsel.
Die notwendige Bedingung reicht also nicht als Nachweis eines Extremwertes aus. Hinreichend ist aber, wenn zusätzlich noch ein Vorzeichenwechsel von f´(x) vorliegt oder dort die Steigung der
1. Ableitung (also die 2. Ableitung) nicht waagerecht – also ungleich Null ist.
Hinreichende Bedingung für Extremstellen :
f´(x) = 0 und zugleich Vorzeichenwechsel von f´(x) bei x0.
Vorzeichenwechsel von + nach – → bei x0 ist ein lokales Maximum.
Vorzeichenwechsel von – nach + → bei x0 ist ein lokales Minimum.
Liegt kein Vorzeichenwechsel vor, so hat f bei x0 einen Sattelpunkt.
Hat f´ an der Stelle x0 einen Vorzeichenwechsel, so muss f´ steigen oder fallen,
d.h. es kann nicht sein, dass die Ableitung von f´ an der Stelle x0 den Wert 0 hat.
Hinreichende Bedingung für Extremstellen x0:
f´(x0) = 0 und zugleich f´´(x0) ≠ 0.
f´(x0) = 0 und f´´(x0) > 0 bedeutet, dass bei x0 ein lokales Minimum ist
f´(x0) = 0 und f´´(x0) < 0 bedeutet, dass bei x0 ein lokales Maximum ist.
f´(x0) = 0 und f´´(x0) = 0 und f´´´(x0) ≠ 0 bedeutet, dass bei x0 ein Sattelpunkt ist.
Hat man mit Hilfe der Hinreichenden Bedingung eine Extremstelle x0 gefunden, kann man dann den zugehörigen Extremwert f(x0) durch Einsetzen von x0 in f berechnen und erhält den sogenannten Extrempunkt M(x0|y0).
Man unterscheidet schließlich noch zwischen lokalen und globalen Extremwerten.
Diese Begriffe sind selbsterklärend:
Ein lokaler Extremwert ist der größte (bzw. kleinste) Funktionswert innerhalb einer bestimmten Umgebung.
Ein globaler Extremwert ist der größte (bzw. kleinste) Funktionswert innerhalb des gesamten Definitionsbereiches.
An den Rändern von Definitionsbereichen (z.B. auch bei abschnittsweise definierten Funktionen) können ebenfalls lokale/globale Maxima/Minima auftreten.
Hierzu berechnet man einfach die Funktionswerte an den entsprechenden Stellen.
Wendestellen, Wendepunkte
Eine Stelle x0 , bei der das Schaubild von f von einer Links- in eine Rechtskurve übergeht (oder umgekehrt) nennt man Wendestelle,
den entsprechenden Punkt W(x0|f(x0) Wendepunkt.

Die Tangente in W an das Schaubild von f nennt man Wendetangente.
Einen Wendepunkt mit waagerechter Tangente nennt man Sattelpunkt.
Da ein Wendepunkt eigentlich eine Extremstelle der 1. Ableitung ist, muss man nur die Berechnung von Extremstellen auf die 1. Ableitung anwenden. Deshalb erhöht sich bei der Berechnung nur der Grad der Ableitung.
Notwendige Bedingung für Wendestellen f´´(x)=0
Hinreichende Bedingung für Wendestellen:
f´´(x)=0 und zugleich Vorzeichenwechsel von f´´(x) bei x0.
Hinreichende Bedingung für Wendestellen:
f´´(x)=0 und zugleich f´´´(x0)≠0.
Beispiel:
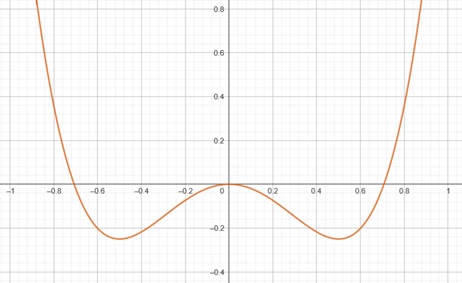
Vollständige Funktionsuntersuchung einer ganzrationalen Funktion 4. Grades
f(x) = 4x4 – 2x2.
- Bestimmung von nach den Ableitungsregeln.
f´(x) = 16x3 – 4x; f´´(x) = 48x2 – 4 ; f´´´(x) = 96x - Symmetrie des Schaubilds:
Achsensymmetrie zur y-Achse, da nur gerade Hochzahlen vorkommen. - Schnittpunkt mit der y-Achse: y = f(0)
f(0) = 4‧04 – 2‧02 = 0 →Sy(0|0) - Nullstellen : f(x) = 0
4x4 – 2x2 = 0 ↔ x2(4x2 – 2) = 0 ↔ x2 = 0˅4x2 – 2 = 0 ↔ x = 0 ˅ x = ±√0,5 - Verhalten für (betrachte den Summanden mit der höchsten Hochzahl)
- lim 4x4 = +∞ oder lim 4x4 = + ∞
x→ +∞ x→ – ∞ - Hoch-/Tiefpunkte:
Bed.: f´(x) = 0
16x3 – 4x = 0 ↔x(16x2 – 4) = 0 ↔x = 0˅x = ±√0,25
hinr.Bed.: f´(x) = 0 ˄ f´´(x) ≠ 0
f´´ (0) = 48‧0 – 4 = -4 < 0 → rel. Max.
f´´(√0,25)= 48‧0,25 – 4 = 8 > 0 → rel. Min.
f´´(-√0,25)=48‧0,25 – 4 = 8 > 0 → rel. Min.
y-Werte: f(0) = 0 ; f(√0,25) = 4‧1/16 – 2‧1/4= – 0,25 = f(-√0,25) wegen Symmetrie
M1(0|0); M2(√0,25|-0,25); M3(-√0,25|-0,25) - Wendepunkte:
Bed.: f´´(x) = 0
48x2 – 4 = 0 ↔48x2 = 4 ↔x = ±√1/12
hinr.Bed.: f´´(x) = 0 ˄ f´´´(x) ≠ 0
f´´´(√1/12)= 96‧√1/12 > 0 → WP(R/L)
f´´´(-√1/12)=96‧(-√1/12) < 0 WP(L/R)
y-Werte: f(√1/12) = 4‧1/144 – 2‧1/12= 1/36 – 6/36 =-5/36 = f(-√1/12) wegen Symmetrie
W1(√1/12|-5/36); W2(-√1/12|-5/36)
Schaubild
Aufgabe 1: Gegeben sei die Funktion f mit f(x) = ¼ x4 + 4/3 x3 + 2x2.
Führen Sie eine vollständige Kurvendiskussion durch!
Aufgabe 2: Gegeben ist die Funktion f mit f(x) = -1/2 x3 + 3x2 + 9/2 x .
- Bestimmen Sie die Wendestelle von f und überprüfen Sie, ob es sich um einen Sattelpunkt handelt.
- Berechnen Sie die Gleichung der Tangente im Wendepunkt.
Aufgabe 3: Die Produktionskosten für die Herstellung eines Produktes lassen sich durch die Kostenfunktion
K mit K(x) = 0,01x3 – 3x2 + 500x +10000 angeben.
Dabei ist x die Produktionsmenge pro Monat und K(x) ist in Euro angegeben.
Der Preis p beträgt 400€ pro hergestellter Produktionseinheit.
Alle hergestellten Produktionseinheiten werden sofort verkauft.
- Geben Sie allgemein an, wie hoch der Gewinn G pro Monat ist.
- Für welche Produktionsmenge wird der Gewinn maximal?
- Für welche Produktionsmengen ergibt sich ein Verlust?
Die Grenzkostenfunktion f(x) ist die 1. Ableitung der Kostenfunktion. Für welche Produktionsmenge werden die Grenzkosten f minimal?
Aufgabe 4: Die Abbildung zeigt die über einen längeren Zeitraum erfasste durchschnittliche Anzahl der momentanen Besucher einer Internetseite im Zeitraum von 6.00Uhr morgens bis 20.00Uhr abends.
- Beschreiben Sie anhand der graphischen Darstellung mit eigenen Worten den Verlauf des Besuchs der Internetseite. Begründen Sie insbesondere, warum die Anzahl der Besucher zuerst ansteigt und dann wieder abfällt.
Der Funktionsterm der Funktion, die die oben dargestellte durchschnittliche Anzahl A der momentanen Besucher der Internetseite in Abhängigkeit von der Zeit t beschreibt, lautet
A(t) = – t3 +30t2 – 225t +520 mit 6 ≤ t ≤ 20 und t in Stunden - Berechnen Sie, wie viele Interessenten die Internetseite um 8.00Uhr durchschnittlich besuchen.
- Berechnen Sie, um wie viele Interessenten sich die Anzahl der Besucher zwischen 8.00Uhr und 9.00Uhr durchschnittlich verändert.
- Berechnen Sie, um welche Uhrzeit durchschnittlich 270 Interessenten die Internetseite besuchen.
- Berechnen Sie, um welche Uhrzeit sich die Anzahl der Besucher durchschnittlich am stärksten vergrößert. Berechnen Sie weiter, wie viele zusätzliche Besucher die Internetseite in der darauffolgenden Stunde durchschnittlich hat.
- Berechnen Sie, um welche Uhrzeit durchschnittlich die meisten Interessenten die Internetseite besuchen. Berechnen Sie weiter, wie viele Interessenten dies durchschnittlich sind.
5.2. Tangenten berechnen
Eine Tangente an den Graphen einer Funktion berührt die Funktion an dieser Stelle. Deshalb haben Funktion und Tangente dort die gleich Steigung, die man ja mit der 1. Ableitung berechnen kann. Zur Tangentenberechnung, die ja eine Gerade ist, braucht man dann noch einen Punkt der Geraden. Meist ist dies der gemeinsame Punkt von Funktion und Tangente – kann aber auch anders gegeben sein.
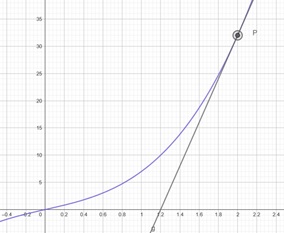
Beispiel: Berechne eine Tangente, die den Graph von f(x) = 3x3 + 4x
an der Stelle x = 2 berührt.
Lösung: Die Tangente ist eine Gerade mit der Gleichung y = mx + b
m ist die Steigung und kann mit der 1. Ableitung
f´(x) = 9x2 + 4 berechnet werden:
m = f´(2) = 9‧4 +4 = 40
b berechnet man mit einem Punkt der Tangente. Dies ist der gemeinsame Berührpunkt an der Stelle x = 2.
y = f(2) = 24 + 8 = 32 →P(2|32)
Einsetzen von m und P in die Tangentengleichung ergibt: 32 = 40‧2 + b ↔b= 32 – 80 = – 48
Dies ergibt die Tangente: y = 40x – 48
Aufgabe 1:
Gegeben ist die Funktion f(x) = 3x2 +12.
- Berechne eine Tangente an die Funktion an der Stelle x = 2.
- Bestimme eine Tangente an die Funktion mit der Steigung m = 4. Wo schneidet diese Gerade die Koordinatenachsen?
- Gibt es eine Gerade y = mx, die die Parabel f(x) nur in einem Punkt schneidet? Wenn ja, berechne die Steigung m und den Punkt, an dem die Gerade die Parabel berührt. Wie nennt man diese Gerade?
Aufgabe 2: Gegeben ist die Funktion f mit
f(x) = x4 – 3x2 + 2.
- Berechne die Tangentengleichung im Punkt P(2;y).
- In welchen Punkten hat die Funktion f(x) die Steigung –2?
Berechne dort eine Tangentengleichung.
5.3. Extremwertaufgaben
Bei Extremwertaufgaben werden größte oder kleinste Werte gesucht, die in einem Sachzusammenhang stehen, den man in eine Funktion überführen muss, von der man dann ein rel. Maximum oder Minimum berechnen muss. Der Sachzusammenhang kann einen geometrischen, wirtschaftlichen, mathematischen oder funktionalen Zusammenhang haben.
Die Vorgehensweise ist dabei oft so, dass man zunächst die Extremalbedingung aufstellt (u.U. mit mehreren Variablen) und mit Nebenbedingungen (durch Einsetzen) die Anzahl der Variablen auf eine Funktionsvariable reduziert.
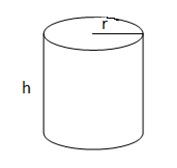
Beispiel: Welche zylindrische Dose mit dem Oberflächeninhalt 1 dm2 hat das größte Volumen?
Lösung: Die Extremalbedingung ist das Volumen
V = G‧h = ¶‧r2‧h (2 Variablen)
Man braucht also noch eine Nebenbedingung.
Dies ist die Oberfläche, die fest vorgegeben ist.
O = 2‧¶‧r2 + M = 2‧¶‧r2 + 2‧¶‧r‧h = 1 dm2
Die Nebenbedingung stellt man nach h um und setzt diese in die Extremalbedingung ein. Man erhält die Zielfunktion, die nur noch eine Variable hat und von der man dann den relativen Extremwert berechnen kann.

Aufgabe 1: Welches oben offene zylindrische Gefäß mit 1 l Fassungsvermögen hat den geringsten Materialverbrauch?


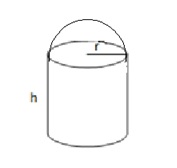
Aufgabe 2: Ein Gefäß besteht aus einem Zylinder mit angesetzter Halbkugel. Welche Form muss es haben, damit es ohne Deckel bei gegebener Oberfläche ein möglichst großes Volumen hat?
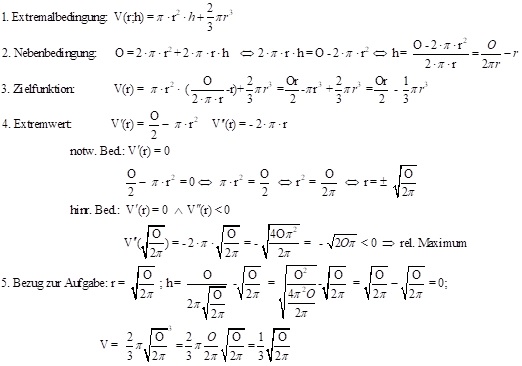
Aufgabe 3: Welcher Punkt des Graphen der Funktion f(x) = 1/x hat vom Koordinatenursprung minimalen Abstand?

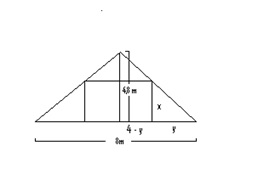
Aufgabe 4: Ein Dachboden hat als Querschnittsfläche ein gleichschenkliges Dreieck mit einer Höhe von 4,8 m und einer Breite von 8 m. In ihm soll ein möglichst großes quaderförmiges Zimmer eingerichtet werden.

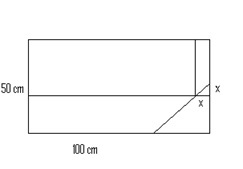
Aufgabe 5: Aus einer rechteckigen Fensterscheibe mit den Seitenlängen a=50 cm und b=100 cm ist vom Mittelpunkt der kleineren Seite aus eine Ecke unter einem Winkel von 45o abgesprungen. Aus der restlichen Scheibe soll durch Schnitte parallel zu den ursprünglichen Seiten eine möglichst große Scheibe hergestellt werden. Gib die Maße der neuen Scheibe an.

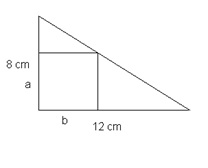
Aufgabe 6: Die Katheten eines rechtwinkligen Dreiecks sind 12 cm und 8 cm lang. Diesem Dreieck ist ein möglichst großes Rechteck einzubeschreiben, von dem zwei Seiten auf den Katheten des Dreiecks liegen.

5.4. Funktionsscharen
Oft verlaufen Funktionen ähnlich und unterscheiden sich nur durch ihre Größe oder Höhe. Damit man sie nicht einzeln untersuchen und berechnen muss, fasst man diese Funktionen zu einer Funktionsschar zusammen, in dem man eine weitere Variable im Funktionsterm einführt. Dies ist dann aber keine Funktionsvariable, die nach den Regeln abgeleitet wird, sondern diese Variable wird wie eine Konstante behandelt. Durch Einführung eines solchen Parameters entstehen unendlich ähnlich verlaufende Funktionsgraphen.
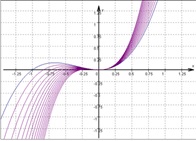
Beispiel:
Vollständige Funktionsuntersuchung der Funktionenschar ft(x) = – 1/18 x4 + 1/3 tx3 ; t Є ℝ+
- Ableitungen:
f´t (x) = – 2/9 x3 + tx2 f´´t (x) = – 2/3 x2 + 2tx f´´´t (x) = –4/3 x + 2t - Symmetrie:
Es ist keine Symmetrie erkennbar, da sowohl gerade als auch ungerade Hochzahlen vorkommen. - Nullstellen und y-Achsenschnittpunkt:
Nullstellen: ft(x) = 0
–1/18 x4 + 1/3 tx3 = 0 ↔ (–1/18 x + 1/3 t)x3 = 0 ↔x1 = 0 ; x2 = 6t →N1(0|0), N2(6t|0)
y-Achsenschnittpunkt: y = ft(0)
ft(0) = 0 →Sy(0|0) - Verhalten für x → ±∞
Bei Polynomen ist dafür der Summand mit der größten Hochzahl verantwortlich, also verhält sich die Funktion wie gt(x) = –1/18 x4
lim (–1/18 x4) = – ∞ oder lim (–1/18 x4) = – ∞
x→ +∞ x→ – ∞ - Extremstellen:
Überprüfe zuerst die notwendige Bedingung: f´t(x) = 0;
–2/9x3 + tx2 = 0 → x2(–2/9x3 + tx2) = 0 → x1 = 0; x2 = 9/2t
Überprüfe dann zusätzlich die hinreichende Bedingung f´t(x) = 0 und f´´t(x) ≠ 0:
f´´t(0) = -2/3‧02 + 2t‧0 = 0 → keine Aussage, ob x1= 0 Extremstelle ist.
f´´´t(0) = -4/3‧0 + 2t = 2t ≠ 0 für t ≠ 0 → Sattelpunkt
= 0 für t = 0; f(4)0(0) = -4/3 < 0 → rel Maximum (einziges Maximum)
f´´t(9/2t) = -2/3‧(9/2t)2 + 2t‧9/2 = -9/2t2 < 0 → Maximum an der Stelle x2 = 9/2t
Berechne die Funktionswerte:
ft(0) = 0 → S(0|0);
ft(9/2t) = -1/18‧(9/2t)4 + 1/3t‧(9/2t)3 = 243/32t4 = 7,59375t4 →H(9/2t|243/32t4) - Wendestellen:
Überprüfe zuerst die notwendige Bedingung: ft´´(x) = 0
-2/3x2 + 2tx = 0 → x(-2/3x +2t) = 0 →x1 = 0 ; x2 = 3t
Überprüfe dann zusätzlich die hinreichende Bedingung: ft´´(x) = 0 und ft´´´(x) ≠ 0
ft´´´(0) = -4/3‧0 + 2t = 2t ≠ 0 →Wendestelle für t≠0
Da auch f´t(0) = 0 ist, ist hier ein Sattelpunkt W1(0|0).
ft´´´(3t) = -4/3‧3t + 2t = -2t ≠ 0 →Wendestelle für t ≠ 0
Berechne den Funktionswert an der Stelle x = 3t:
ft(3t) = -1/18‧(3t)4 + 1/3t‧(3t)3 = 9/2t4= 4,5t4 →W2(3t|4,5t4)
Zusammenstellung der Ergebnisse und Schaubild:
Das unsymmetrische Schaubild von ft hat zwei Nullstellen N1(0|0) und N2(6t|0),
einen Hochpunkt: H(9/2t| 243/32t4), zwei Wendepunkte W1(0|0) und W2(3t|4,5t4);
wobei W1(0|0) ein Sattelpunkt ist,
- Beispiele:
t = 1 → f1(x) = -1/18x4 + 1/3x3
N1(0|0), N2(6|0), H(4,5|7,6), W1(0|0), W2(3|4,5)
t = 0,5 →f0,5(x) = -1/18x4 + 1/6x3
N1(0|0), N2(3|0), H(2,25|0,47), W1(0|0), W2(1,5|0,28)
Aufgabe: Untersuche allgemein den Funktionsverlauf der Funktionsschar fk(x) = x4 + kx3. Bestimme zusätzlich die Ortslinien, auf denen die Extrempunkte und Wendepunkte liegen.


5.5. Vermischte Aufgaben
Aufgabe 1:
Eine Kugel, die eine schiefe Ebene hinunterrollt, wird immer schneller. Dabei wird angenommen, dass für den zur Zeit x in Sekunden der zurückgelegte Weg s in Metern gilt:
s(x) = 0,2×x2.
- Berechne die Durchschnittsgeschwindigkeit zwischen 0 und 8 Sekunden.
- Bestimme die Momentangeschwindigkeit nach 2, 4, 6 und 8 Sekunden.
Aufgabe 2:
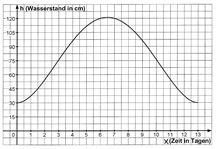
Während einer Hochwasserwelle wurde in einer Stadt der Wasserstand h des hochwasserführenden Flusses in Abhängigkeit von der Zeit x gemessen. Die nebenstehende Graphik zeigt die graphische Darstellung der Messwerte. Der Funktionsterm der Funktion, die den zeitlichen Verlauf der Hochwasserwelle beschreibt, lautet:
H(x) = 5/98 x4 – 65/49 x3 + 845/98 x2 + 30 mit 0 ≤ x ≤ 13
a) Berechne die durchschnittliche Wasserstandsänderung pro Tag vom Beginn bis zum 5. Tag und vom 7. bis zum 12. Tag.
b) Wo hoch ist der Wasseranstieg am 4. Tag? Mit welcher stündlichen Wasserstandsänderung ist zu rechnen?
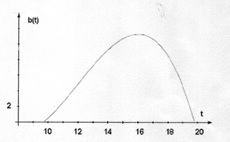
Aufgabe 3:
Die nebenstehende Graphik gibt vereinfacht die Anzahl b der Besucher (gemessen in tausend Personen) in einem Freizeitpark von 10.00 Uhr bis 19.30 Uhr an. Der Funktionsterm lautet:
b(x) = -0,05x3 + 1,8x2 – 19,2x + 62,5 mit 10 < x < 19,5
a) Wie groß ist die durchschnittliche Besucherzahländerung pro Stunde in der Zeit von 10 bis 14 Uhr?
b) Berechne die momentane stündlicher Besucherzahländerung um 12 Uhr 30 und 17 Uhr 30.
c) Es muss eine weitere Kasse aufgemacht werden, wenn stündlich mehr als 2250 Besucher in den Park wollen. Wann muss man eine weitere Kasse besetzen?
Aufgabe 4: Gegeben ist die Funktion f(x) = 1/12 x4 – 9/2 x2.
- Führe eine komplette Kurvendiskussion durch.
- Berechne die Wendetangenten.
- Berechne den Schnittpunkt der Wendetangenten.
- Bestimme die beiden Geraden, die ein rel. Minima und ein rel. Maxima miteinander verbinden.
Aufgabe 5:
- Gib die Ableitungsfunktion an.
a) f(x) = 4x5 + 6x3 + 1 d) f(x) = (x + 3)3 g) f(x) = √x +1/x
b) f(x) = 1/8 x3 + ½ x e) f(x) = 5x + 2 h) f(x) = 1/x3
c) f(x) = x(x+1)(x-2) f) f(x) = √4 ‧x2 i) f(x) = 2(x+2)2 - Gib die Funktion f an.
a) f´(x) = 7x6 b) f´(x) = 14 x13 + 4 x3 c) f´(x) = x6 + 2
Aufgabe 6:
Gegeben ist die Funktion f(x) = 12x3 – 14.
- Bestimme die Gleichung der Tangente von f im Punkte P(2/y).
- Bestimme die Gleichung der Tangente von f mit der Steigung 36.
- Bestimme die Gleichung der Tangente von f mit dem Steigungs-winkel a = 45°.