7. Hypothesentest
7.1 Entscheidungsregel
Bei einer Entscheidungsregel stellt man eine bestimmte Behauptung auf und überprüft mit einer ausreichend großen Stichprobe die Richtigkeit dieser Behauptung. Man kann davon ausgehen, dass die Behauptung stimmt, wenn das Ergebnis der Stichprobe nicht signifikant vom Erwartungswert abweicht. Dies ist der Fall, wenn das Ergebnis im 95% Bereich liegt.
Beispiel für einen Minimalwert:
Ein Unternehmen möchte erreichen, dass mindestens 30% der Menschen ihr Produkt kennen. Sie überlegen eine Werbekampagne zu starten, falls dies noch nicht der Fall ist. Bei 1000 Befragten müsste man 300 Personen erwarten, die das Produkt kennen. Die Kampagne wird gestartet, wenn das Ergebnis der Untersuchung signifikant nach unten dazu abweicht, d.h. mit 5% Wahrscheinlichkeit darunter liegt. Bis zu welcher Personenanzahl geht dieser Bereich, so dass eine Kampagne gestartet werden muss?
BinominalCD(280,1000,0,3)=0,0886
BinominalCD(276,1000,0,3)=0,0516
BinominalCD(275,1000,0,3)=0,0446
Das Ereignis 0 ≤ n ≤ 275 tritt nur mit einer Wahrscheinlichkeit von 4,5% ein. Liegt die Untersuchung in diesem Bereich, so muss eine Werbekampagne gestartet werden.
Beispiel für einen Bereich um einen Erwartungswert:
Eine Schokoladenfirma glaubt, dass sie ihren Marktanteil von 27% aller Schokoladen in einem Supermarkt gehalten hat. Die Firma überprüft nun bei den nächsten 500 Käufern einer Schokolade, ob das Ergebnis signifikant abweicht. Das Ergebnis könnte dabei oberhalb oder unterhalb des Erwartungswerts liegen. Deshalb teilt man hier die 5% auf beide Bereiche auf.
BinominalCD(115,500,0,27)=0,0233
BinominalCD(116,500,0,27)=0,0298
BinominalCD(155,500,500,0,27)=0,0259
BinominalCD(156,500,500,0,27)=0,0206
Der Bereich zwischen 116 und 155 hat eine Wahrscheinlichkeit von 95 %. In diesem bereich geht man dann davon aus, dass diese Behauptung stimmt. Ergebnisse außerhalb sind signifikant abweichend vom Erwartungswert μ = 135.
7.2 Hypothesentest
Ein Hypothesentest ist ein statistisches Testverfahren, bei dem man eine Hypothese aufstellt, die mit einer Untersuchung überprüft werden soll. Man bestimmt zu der Hypothese einen Annahmebereich A und einen Verwerfungsbereich V und formuliert eine Entscheidungsregel. Danach kann man auch noch die Wahrscheinlichkeiten eines Fehlers berechnen.
Man muss bei den Hypothesentests zunächst mal eine Hypothese aufstellen. Hier unterscheidet man eine Nullhypothese H0, bei der die Gleichheit enthalten ist
(p = p0; p ≥ p0; p ≤ p0) oder die Alternativhypothese H1, bei der es nur größer oder kleiner gibt.
Nach dem Aufstellen der Nullhypothese muss der Annahme- und Ablehnungsbereich für das Testverfahren aufgestellt werden. Diese Bereiche sind nicht willkürlich zu wählen, man muss dazu ein Signifikanzniveau α festlegen, um zu entscheiden, ob ein Test signifikant vom Normalen abweicht. Ist das Signifikanzniveau 5%, so liegen 95% im Annahmebereich und nur 5% im Ablehnungs- bzw. Verwerfungsbereich.
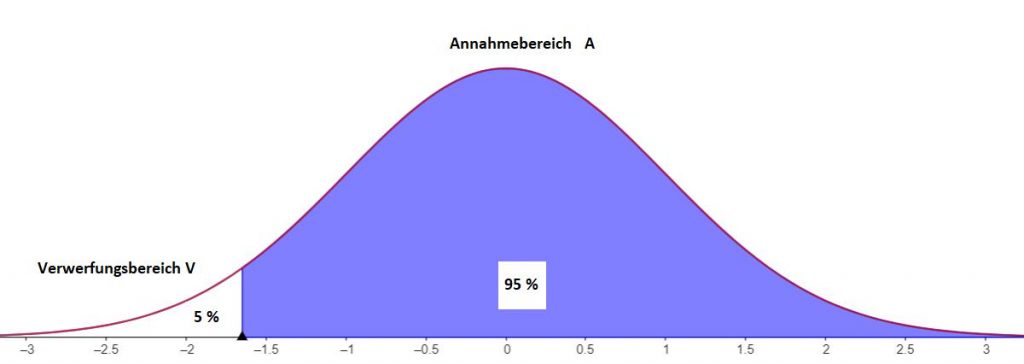
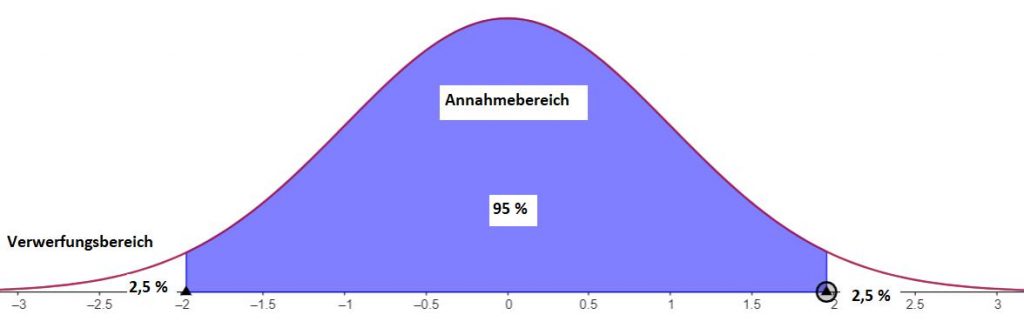
Bei einem Hypothesentest kann es einen einseitigen (größer gleich oder kleiner gleich) oder zweiseitigen (Intervall) Hypothesentest geben.
7.3 Fehler 1. und 2. Art
Ein Fehler 1. und 2. Art sind statistische Fehlentscheidungen bei Hypothesentests. Sie beziehen sich auf die Situation, in der man eine Hypothese über einen unbekannten Parameter annehmen oder ablehnen muss, basierend auf einer Stichprobe von Daten.
Eine Hypothese kann niemals eindeutig bewiesen oder widerlegt werden. Es treten beim Testen immer Fehler auf, die wir im Folgenden als Fehler 1. und 2. Art bezeichnen.
Ein Fehler 1. Art liegt vor, wenn man die Nullhypothese ablehnt, obwohl sie wahr ist. Diese Wahrscheinlichkeit für einen Fehler 1. Art wird mit α bezeichnet und wird auch Irrtumswahrscheinlichkeit genannt.
Ein Fehler 2. Art liegt vor, wenn man die Nullhypothese annimmt, obwohl sie falsch ist. Die Wahrscheinlichkeit für einen Fehler 2. Art wird mit β bezeichnet und wird auch Risiko genannt.
Folgende Fälle können dann beim Testen auftreten:
Der Fehler 1. Art wird meist in der Aufgabenstellung angegeben. Beim Fehler 2. Art liegt in Wirklichkeit eine andere Wahrscheinlichkeit vor, mit der man dann die Wahrscheinlichkeit für den Fehler 2. Art berechnen muss.
|
|
H0 wird angenommen |
H0 wird abgelehnt |
|
H0 ist wahr |
Sicherheitsbereich |
Fehler 1. Art α (Signifikanzniveau) |
|
H0 ist falsch |
Fehler 2. Art β |
Sicherheitsbereich |
7.4 Einseitiger Hypothesentest
Ein einseitiger Hypothesentest kann linksseitig oder rechtsseitig sein. Man testet also nur eine Richtung der Abweichung vom Erwartungswert.
Bei einem linksseitigen Hypothesentest wird die Nullhypothese abgelehnt, wenn das Testergebnis kleiner als ein bestimmter Wert ist mit einem Signifikanzniveau α (in der Grafik ist α = 5%).
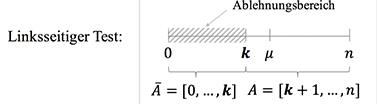
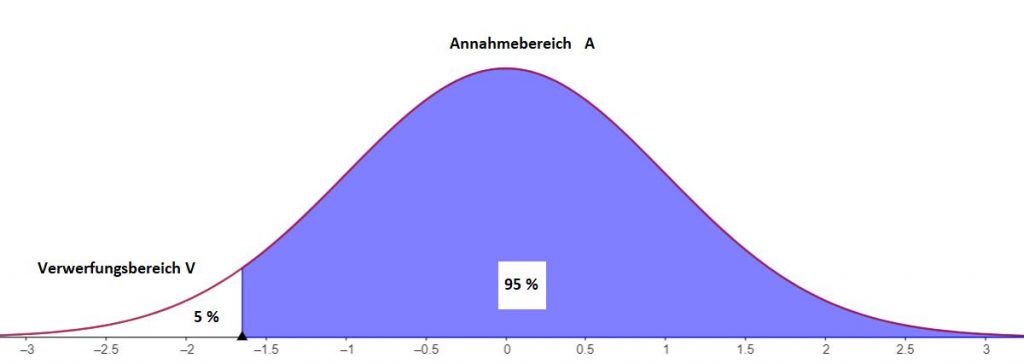
Beispiel: Eine Firma garantiert für sein Produkt, dass mindestens 90% der gelieferten Ware Güteklasse A hat und nur 10% der Ware Güteklasse B hat. Die nächsten 300 Wareneingänge sollen überprüft werden. Formuliere die Nullhypothese und stelle den Annahme und Verwerfungsbereich mit einem Signifikanzniveau von 5% auf. Berechne die Wahrscheinlichkeit für den Fehler 1. und 2. Art.
Lösung: Da man beim Hypothesentest immer einen kritischen Standpunkt einnimmt, wird überprüft, ob mehr als 10% der Ware Güteklasse B hat. H0: p ≥ 0,1
H0: Mindestens 10% der Ware hat Güteklasse B.
Wir benutzen die Binominalverteilung mit p=0,1 n=300 und berechnen einige kumulierten Wahrscheinlichkeiten.
BinominalCD(21,300,0,1)=0,0458
BinominalCD(22,300,0,1)=0,0699
Zwischen 21 und 22 hat man das Signifikanzniveau von 5% erreicht.
Also ist der Verwerfungsbereich [0,21] und der Annahmebereich [22,300].
Der Fehler 1. Art tritt ein, wenn die Nullhypothese stimmt, sie aber abgelehnt wird. Dieser Wert ergibt sich aus dem Signifikanzniveau α = 0,05.
Beim Fehler 2. Art stimmt die Nullhypothese nicht. Wenn nun 9% B-Ware richtig ist, so ergibt sich die Wahrscheinlichkeit für den Fehler 2. Art aus dieser Binominalverteilung für p=0,09.
BinominalCD(22,300,300,0,09)=0,8681
Bei p=0,08 ergibt sich eine Wahrscheinlichkeit für den Fehler 2. Art von
BinminalCD(22,300,300,0,08)=0,6951
Die Wahrscheinlichkeit beim Fehler 2. Art nimmt für kleiner Prozentzahlen immer weiter ab.
Bei einem rechtsseitigen Hypothesentest wird die Nullhypothese abgelehnt, wenn das Testergebnis größer als ein bestimmter Wert ist bei einem bestimmten Signifikanzniveau α (in der Grafik ist α = 5%).

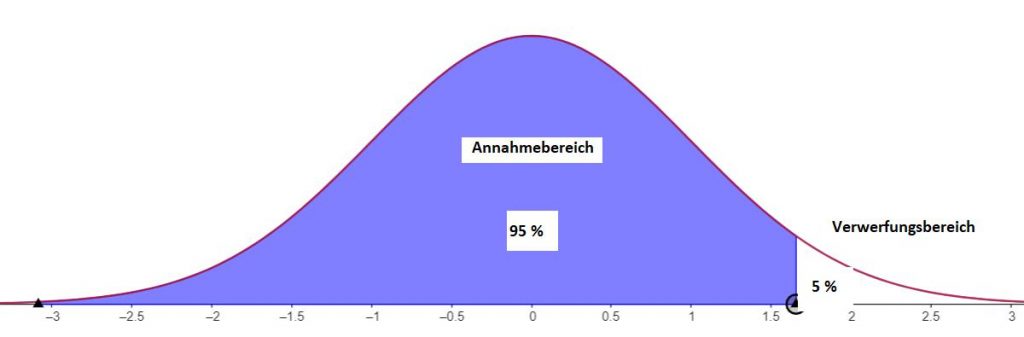
Beispiel: In einer Fabrik werden Platinen produziert. Dabei werden nicht alle Platinen ordnungsgemäß produziert und haben einen Fehler. Stündlich werden 100 Platinen kontrolliert. Erfahrungsgemäß werden nicht mehr als 20% der Platinen fehlerhaft produziert. In einer Stichprobe werden 25 Platinen als fehlerhaft gefunden.
(1) Wie viele fehlerhaften Platinen dürfen höchstens in der Kontrolle gefunden werden? (Irrtumswahrscheinlichkeit = 5%)
(2) Berechne den Fehler 2. Art, wenn tatsächlich 25% der Platinen einen Fehler haben.
Lösung:
(1) n=100; p=0,2; μ = 20
BinominalCD(26,100,0,2)=0,9442
BinominalCD(27,100,0,2)=0,9658
Der Annahmebereich ist [0;27] und der Ablehnungsbereich ist [28;100]
Da σ = √n‧ p‧ (1–p) = 4 > 3 kann man auch die σ-Regel anwenden. Man müsste aber die 90% Umgebung bestimmen, da dieser Hypothesentest nur einseitig ist und man aber die 5% auf beiden Seiten abziehen müsste. Es ist laut Tabelle siehe oben die 1,645σ-Umgenbung.
1,645‧4=6,616. Somit muss man auf den Erwartungswert μ = 20 6,616 addieren und erhält 26,616. Bei dieser Rechnung liegt die Grenze für den Annahmebereich auch bei 27.
(2) n=100; p=0,25
β=BinominalCD(27,100,0,25)= 0,7224
7.5 Zweiseitiger Hypothesentest
Ein zweiseitiger Hypothesentest testet in beide Richtungen. Man prüft, ob die Nullhypothese richtig oder falsch ist ohne anzugeben, ob das Ergebnis größer oder kleiner ist. Der Ablehnungsbereich der Nullhypothese liegt bei einem zweiseitigen Hypothesentest auf beiden Seiten des Erwartungswerts.

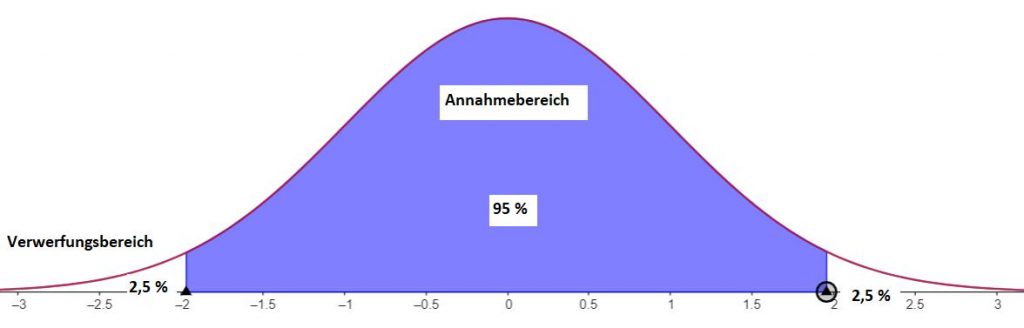
Beispiel 1:
Es werden Fußballfans in einer Stadt betrachtet. Dabei machen 20% die Fans einer Mannschaft A aus, die anderen halten auf Mannschaft B. Wir nehmen nun eine Stichprobe von 160 Fußballfans dieser Stadt (Signifikanzniveau: 5%).
In der Stichprobe befinden sich 44 Fußballfans der Mannschaft A und 116 der Mannschaft B.
- Kann H0verworfen werden?
- Berechne die Wahrscheinlichkeit für den Fehler 1. und 2. Art, wenn der tatsächliche Anteil der Fans von A 30% beträgt.
Lösung a)
- Der Erwartungswert ist μ = n‧p = 160‧0,2 = 32
Die Standardabweichung ist σ = √n‧p‧(1–p) = √160‧0,2‧0,8 = 5,06 > 3 - Da man also die σ-Regel anwenden darf, liegen 95% in der 1,96σ-Umgebung um den Erwartungswert.
32–1,96σ=32–9,92=22,08 und 32+9,92=41,92. - Der Annahmebereich ist also [23;41] und der Ablehnungsbereich ist also bis 22 und ab 42.
- Bei 44 Fans der Mannschaft A liegen wir also im Ablehnungsbereich. H0 wird also verworfen.
Lösung b)
- Der Fehler 1. Art ist also die Irrtumswahrscheinlichkeit, die bei 5% liegt.
- Der Fehler 2. Art wird mit p=0,3 und n=160 berechnet,
- BinominalCD(23,41,160,0.3)=0,1303
Da es keine Tabelle für n = 160 gibt und die Laplace-Bedingung erfüllt ist, können wir die Binomialverteilung durch die Normalverteilung approximieren. Da eine Approximation von der Binomialverteilung (diskret) zur Normalverteilung (stetig) vorliegt, müssen Stetigkeitskorrekturen beachtet werden.
- Es folgt: μ=160‧0,3=48 und σ = √160‧0,3‧0,7=5,8
- P(a≤X≤b) = Φ((b+0,5-μ)/σ) – Φ((a–0,5-μ)/σ)
P(23≤X≤41) = Φ((41+0,5–48)/5,8)- Φ((23–0,5-48)/5,8)=
Φ(–1,12) –Φ(–4,40)= NormCD(–4, –1.12,1,0)=0,1314 - Hat man nur positive Werte in der Tabelle, so muss man noch umrechnen:
Φ(–1,12)-Φ(–4,40)= 1–Φ(1,12)-(1-Φ(4,40))=0,6314-0,5=0,1314
Beispiel 2: Eine Maschine produziert 500 mm lange Schrauben mit einer Standardabweichung von 10mm. Die Länge der Schrauben kann als normalverteilt angesehen werden.
- Berechne die Wahrscheinlichkeit dafür, dass eine Schraube kürzer ist als 485 mm.
- Berechne die Wahrscheinlichkeit dafür, dass eine Schraube höchstens 501mm und mindestens 499mm lang ist.
Lösung:
a) Die Länge der Schrauben ist normalverteilt mit dem Erwartungswert μ=500 und der Standardabweichung σ=10. Gesucht ist die Wahrscheinlichkeit dafür, dass eine Schraube kürzer ist als 485 mm, also P(X≤485).
P(X≤k)≈Φ((k−μ)/σ); P(X≤485)≈Φ((485−500)/10)=Φ(−1.5)=1−Φ(1,5)≈1−0,93319=0.06681
Die Wahrscheinlichkeit dafür, dass eine Schraube kürzer als 4,85cm ist, beträgt also etwa 6,7%.
b) Die Länge der Schrauben ist normalverteilt mit Erwartungswert μ=500 und Standardabweichung σ=10. Gesucht ist die Wahrscheinlichkeit dafür, dass eine Schraube länger ist als 499mm und kürzer als 501mm, also P(499≤X≤501).
P(499≤X≤501)=P(X≤501) −P(X≤499)≈Φ((501−500)/10)−Φ((499−500)/10)=
Φ(0,1)−Φ(−0,1)=Φ(0,1)−Φ(−0,1)=Φ(0,1)−(1−Φ(0,1))=Φ(0,1)−(1−Φ(0,1))
≈0,53983−(1−0,5383)=0,08≈0,53983−(1−0,5383)=0,08
Die Wahrscheinlichkeit dafür, dass eine Schraube höchstens 501mm und mindestens 499mm lang ist, beträgt also etwa 8%.
7.6 Aufgaben
Aufgabe 1: Die Körpergröße von Männern ist normalverteilt mit dem Erwartungswert μ = 178 cm und der Standardabweichung σ = 8 cm.
- Berechne die Wahrscheinlichkeit, dass ein Mann höchstens 170 cm groß ist. Wie groß ist die Wahrscheinlichkeit, dass ein Mann mindestens 190 cm.
- Ermittle, wie groß ein Mann sein muss, damit er
– zu den 20 % kleinsten gehört
– zu den 10 % größten gehört. - Gib ein um den Erwartungswert symmetrisches Intervall an, in dem die Größen von 95 % aller Männer liegen.

Aufgabe 2: Das Gewicht von neugeborenen Kindern ist annähernd normalverteilt mit einem Erwartungswert von μ = 3300 g und einer Standardabweichung von σ = 575 g.
- Berechne die Wahrscheinlichkeit, dass ein Neugeborenes
– mehr als 3000 g wiegt
– weniger als 2500 g wiegt
-zwischen 4000 und 5000 g wiegt. - Wie schwer muss ein Neugeborenes sein, damit es
– zu den 15 % schwersten
– zu den 25 % leichtesten gehört? - In welchem um μ symmetrischen Bereich liegen die Gewichte von 90% aller Neugeborenen?

Aufgabe 3: Die Äpfel in einer Lieferung wiegen durchschnittlich 180 g, mit einer Standardabweichung von 50 g. Man kann annehmen, dass das Gewicht eine normalverteilte Zufallsvariable ist.
- Wieviel Prozent der Äpfel wiegen
– weniger als 150 g (27,41 %)
– mehr als 175 g (53,98 %)
– zwischen 200 und 250 g? (26,38 %) - 10% der Äpfel werden aussortiert, weil sie zu leicht sind. Wie schwer kann ein Apfel höchstens sein, wenn er aussortiert wird? (116 g)
- In welchem symmetrischen Bereich [μ – ε, μ + ε] liegen die Gewichte von 50% aller Äpfel?
(146 g bis 214 g)
Aufgabe 4: Der Intelligenzquotient (IQ) ist eine normalverteilte Zufallsvariable mit dem Erwartungswert μ = 100 und einer Standardabweichung von 15.
- Berechne die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person einen IQ zwischen 90 und 120 hat. (P(90 ≤ X ≤ 120) = 0,656)
- Welchen IQ muss man haben, um zu den intelligentesten 2% der Bevölkerung zu gehören?
(131)
Aufgabe 5: Nüsse werden in Tüten verpackt. Das Füllgewicht ist normalverteilt mit dem Erwartungswert μ = 200 g und einer Standardabweichung von 20g. Wie groß ist die Wahrscheinlichkeit, dass eine zufällig ausgewählte Tüte 196 g bis 205 g enthält.
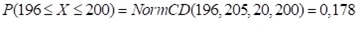
Aufgabe 6: Die durchschnittliche Schlafdauer von Erwachsenen ist normalverteilt mit dem Erwartungswert μ = 7,5 h und der Standardabweichung σ = 0,9 h.
- Berechne die Wahrscheinlichkeit, dass ein Erwachsener weniger als 6 h schläft. (0,048)
- Erkläre, warum die Wahrscheinlichkeit für weniger als 6 h Schlaf genauso groß ist wie die Wahrscheinlichkeit für mehr als 9 h Schlaf. (6 h und 9 h liegen gleich weit vom Erwartungswert entfernt. Wegen der Symmetrie der Normalverteilung sind die beiden Wahrscheinlichkeiten gleich groß.)
- Ermittle die Schlafdauer, die von 20 % aller Erwachsenen überschritten wird.
(8,26 h)
Aufgabe 7: Die Masse der Eier auf einem Hühnerhof ist annähernd normalverteilt. Dabei ist der Erwartungswert μ=65g bei einer Standardabweichung von σ=5g. Berechne die Wahrscheinlichkeit, dass ein Ei zwischen 60 g und 70 g wiegt.
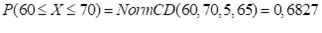
Aufgabe 8: Eine Maschine erzeugt Holzplatten, die im Mittel 30 mm dick sind. Die Standardabweichung beträgt 0,6 mm.
- Bei wieviel Prozent aller Platten liegt die Dicke zwischen 29,5 und 30,5 mm? (59,35 %)
- Wie groß ist die Wahrscheinlichkeit, dass eine Platte dicker als 31 mm ist? (0,0475)
Aufgabe 9: Die Lebensdauer eines Ersatzteils ist normalverteilt, mit μ = 180 Tage und σ = 40 Tage.
- Wie groß ist die Wahrscheinlichkeit, dass die Lebensdauer weniger als 3 Monate beträgt? (1 Monat = 30 Tage) (0,0122)
- Bei wieviel Prozent aller Teile weicht die Lebensdauer um weniger als 1 Monat vom Erwartungswert ab? (54,67 %)
Aufgabe 10: Eine Maschine stellt Nägel her. Die Länge der Nägel ist normalverteilt mit dem Erwartungswert μ = 8,00 cm und der Standardabweichung σ = 0,15 cm.
- Bei wieviel Prozent der Nägel weicht die Länge höchstens um 0,20 cm vom Erwartungswert μ ab? 81,8 %
- Wie sind die Toleranzgrenzen festgelegt, wenn man weiß, dass 90% der Produktion zum Verkauf freigegeben werden? ) 8,00 ± 0,25 cm
Aufgabe 11: Eine faire Münze wird 80 mal geworfen. X ist die Anzahl der Würfe mit dem Ergebnis „Kopf“.
- Ermittle Erwartungswert und Standardabweichung für die Anzahl von „Kopf“.
(μ = 40, σ = 4,47) - Berechne die Wahrscheinlichkeit, 36 bis 42 mal „Kopf“ zu werfen
(1) mit Binomialverteilung, (2) mit Normalverteilung (ohne Stetigkeitskorrektur) (3) mit Normalverteilung (mit Stetigkeitskorrektur). ((1) 0,5546 (2) 0,4871 (3) 0,5548) - Begründe, dass du hier mit Normalverteilung rechnen darfst. )
(Man darf mit Normalverteilung rechnen, weil σ > 3 ist) - Gib einen symmetrischen 90 %-Streubereich für die Anzahl von „Kopf“ an. (33 bis 47)
Aufgabe 12: 7% aller Eier werden beim Transport beschädigt. Ein Geschäft bekommt eine Lieferung von 1500 Eiern.
- Berechne die Wahrscheinlichkeit, dass 120 oder mehr Eier beschädigt sind.
(1) mit Binomialverteilung, (2) mit Normalverteilung (ohne Stetigkeitskorrektur) (3) mit Normalverteilung (mit Stetigkeitskorrektur). ((1) 0,0733 (2) 0,0645 (3) 0,0711) - In welchem symmetrischen Bereich liegt mit 95% Wahrscheinlichkeit die Anzahl der beschädigten Eier? (85 bis 125)
Aufgabe 13: Die freiwillige Feuerwehr eines Ortes verfügt über 120 Feuerwehrleute, von denen jeder mit 60% Wahrscheinlichkeit sofort verfügbar ist.
- Wie groß ist die Wahrscheinlichkeit, dass im Ernstfall mindestens 70 Feuerwehrleute zur Verfügung stehen?
(1) mit Binomialverteilung, (2) mit Normalverteilung (ohne Stetigkeitskorrektur) (3) mit Normalverteilung (mit Stetigkeitskorrektur). ((1) 0,6810 (2) 0,6443 (3) 0,6808) - Gib einen 90%-Streubereich [μ – ε, μ + ε] für die Anzahl der verfügbaren Feuerwehrleute an!
[63; 81]
Aufgabe 14: Ein Passagierflugzeug hat 180 Plätze. Erfahrungsgemäß erscheinen nur 90 % der Passagiere, die einen Platz gebucht haben, auch tatsächlich zum Abflug.
- In welchem Bereich liegt mit 95 %iger Wahrscheinlichkeit die Anzahl der tatsächlich belegten Plätze bei einem ausgebuchten Flug? [154; 170]
- Um leere Plätze zu vermeiden, ist es üblich, dass die Flüge überbucht werden (d.h. es werden mehr Sitzplätze verkauft, als zur Verfügung stehen). Wie groß ist die Wahrscheinlichkeit, dass bei einer 10 %igen Überbuchung nicht alle erscheinenden Fluggäste transportiert werden können?
(1) mit Binomialverteilung, (2) mit Normalverteilung (ohne Stetigkeitskorrektur) (3) mit Normalverteilung (mit Stetigkeitskorrektur). ((1) 0,3008 (2) 0,2536 (3) 0,2929) - Wie viele Buchungen dürfen angenommen werden, wenn das Risiko, einen Passagier abweisen zu müssen, höchstens 1 % betragen soll? (190)