6. Normalverteilung
Bei der Binominalverteilung betrachten wir diskrete Zufallsgrößen mit ganzzahligen x-Werten. Hat man aber Zufallsgrößen mit beliebigen reellen Zahlen, so spricht man von einer stetigen Zufallsgröße wie z.B. Körpergrößen, Geschwindigkeiten, Gewichte, usw. .
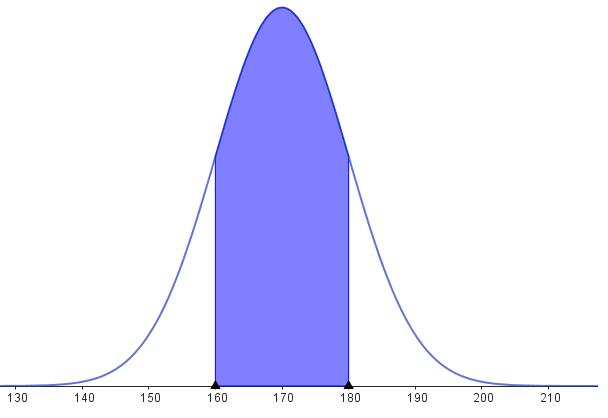
Hier wird die Wahrscheinlichkeitsverteilung der Körpergröße bei Frauen dargestellt. Die höchste Wahrscheinlichkeit ist beim Erwartungswert 170cm mit einer Standardabweichung von 10cm. Je weiter man sich vom Erwartungswert entfernt, umso niedriger wird die Wahrscheinlichkeit.
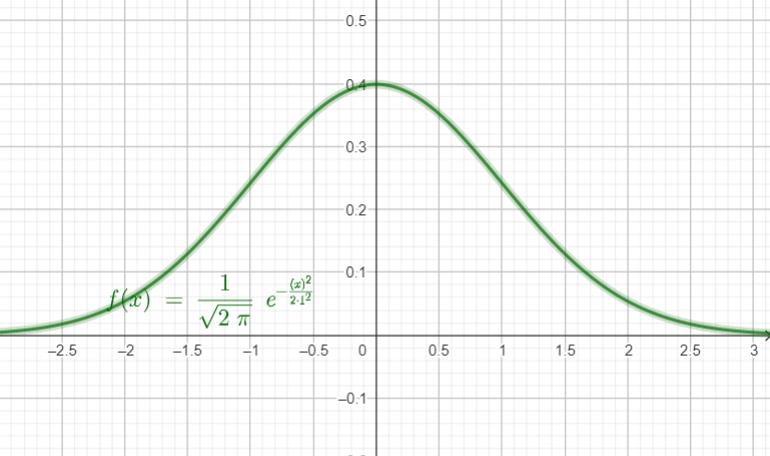
Diese Wahrscheinlichkeiten kann man nicht mehr mit der Bernoulli-Formel berechnen und auch die Summierung für Bereiche funktioniert hier nicht mehr. Man macht sich hier die Tatsache zu Nutze, dass vieles in der Natur normalverteilt ist, d.h. die Wahrscheinlichkeiten bilden als Graphik eine Glockenkurve, der man sich in der Regel mit einer Exponentialfunktion annähern kann. Da die Glockenkurve den Erwartungswert als relatives Maximum hat und die Wendepunkte der Kurve bei den Werten liegen, wenn man die Standardabweichung addiert oder subtrahiert, erhält man bei normalverteilten Zufallsgrößen die Wahrscheinlichkeitsfunktion, die Gauß´sche Glockenkurve.

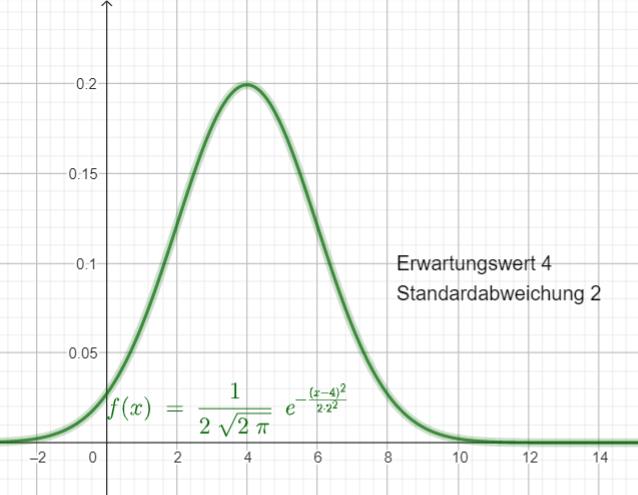
Mit Hilfe dieser Exponentialfunktion kann man nun Wahrscheinlichkeiten für bestimmte Bereich (Intervalle) berechnen, indem man nun die Fläche unter diesem Funktionsgraphen bestimmt. Leider lässt sich die Integralfunktion hiervon nicht berechnen. Wir bezeichnen sie aber mit Φμ,σ(x).
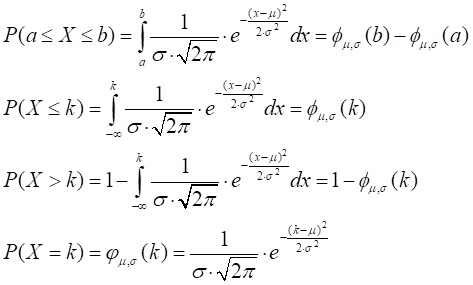
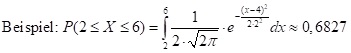
Dieses Ergebnis erhält man auch mit dem Taschenrechner unter NormCD(2,6,2,4)≈0,6827
Allgemein muss man hier eingeben: NormCD(a,b,σ,μ) für das Intervall von a bis b und die Standardabweichung σ und den Erwartungswert μ.
6.1 Normalverteilung als Näherung für die Binominalverteilung
Besonders für sehr hohe Werte oder Werte, die man nicht in der Tabelle nachschlagen kann, kann man die Binominalverteilung durch eine Normalverteilung annähern und die Wahrscheinlichkeiten auch mit Hilfe der Dichtefunktion (Gauß´sche Glockenkurve) näherungsweise berechnen. Da bei der Darstellung einer Binominalverteilung das Histogramm mit Rechtecken der Breite 1 dargestellt werden, bekommt man eine bessere Annäherung, wenn man die Mitte der Rechtecke als Integralgrenzen nimmt. Statt a nimmt man a – 0,5 als untere Grenze und statt b nimmt man b + 0,5 als obere Grenze.
Es gilt der Satz von Moivre-Laplace:
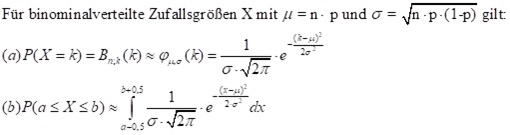
6.2 Standardisierte Normalverteilung
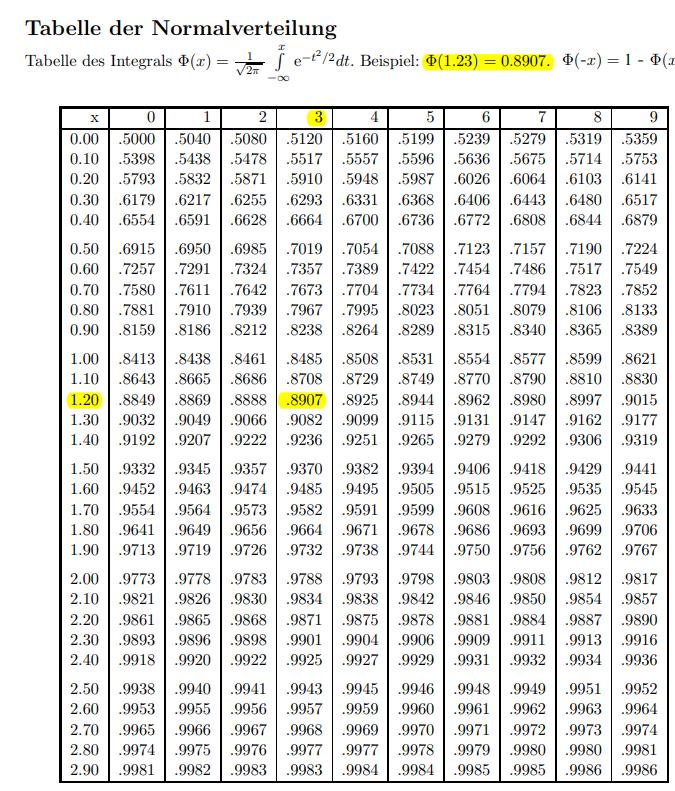
Für dieses Integral der Normalverteilung lässt sich leider keine Stammfunktion bestimmen. Es kann nur Näherungsweise mit dem Rechner bestimmt werden. Hat man keinen Rechner zur Verfügung, so kann man sich Tabellen für diese Integralfunktion zu Nutze machen. Damit man nicht für jeden Erwartungswert und jede Standardabweichung eine andere Tabelle braucht, führt man diese Berechnung auf eine sogenannte Standardnormalverteilung zurück. Bei der standardisierten Normalverteilung ist der Erwartungswert μ = 0 und die Standardabweichung σ = 1.
Die Integralfunktion dieser standardisierten Normalverteilung nennt man nur Φ(x), wobei das Integral von -∞ bis x berechnet wird. Damit man nicht für jede Verteilung eine eigene Tabelle braucht, kann man die alle Werte umrechnen und diese Werte dann mit der standardisierten Normalverteilung Φ(x) nachschlagen. Zu den allgemeinen Normalverteilungen besteht nun folgender Zusammenhang:
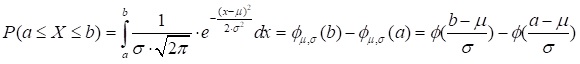
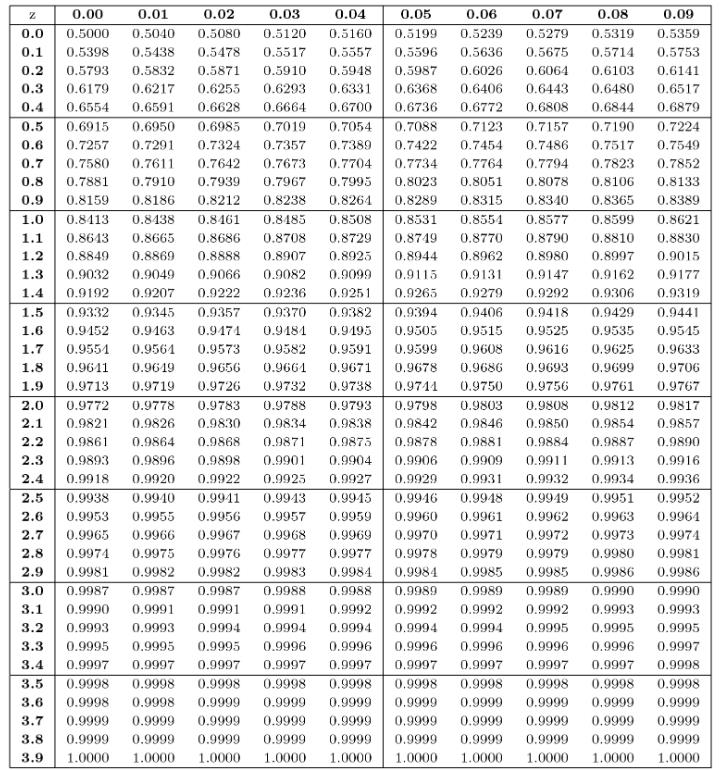
Man muss also nur die Grenzen umrechnen, um die standardisierte Normalverteilung zu benutzen. Bei der Umrechnung können aber auch negative Werte herauskommen. Dann muss man mit dem Gegenereignis die positiven Werte in der Tabelle nachschlagen und danach umrechnen. Es gilt:
Φ(–a) = 1 – Φ(a)
Zur besseren Annäherung nimmt man häufig nicht die Grenzen a und b, sondern man geht auf die Mitten der ganzzahligen Grenzen. Bei der unteren Grenze wird a – 0,5 genommen und bei der oberen Grenze b + 0,5.
Beispiel: Bei einer Untersuchung wird festgestellt, dass die Körpergröße von Männern zwischen 20 und 25 Jahren 1,80 m bei einer Standardabweichung von 9 cm beträgt. Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Mann zwischen 20 und 25 Jahren zwischen 1,75 und 1,85 groß ist?
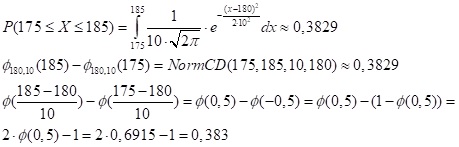
Wahrscheinlichkeit beträgt also immer 38,29%, egal wie man es berechnet.
6.3 Intervallbestimmung durch Umkehrung der Normalverteilung
Mit der inversen Normalverteilung lassen sich Schwellenwerte berechnen, unterhalb dieser eine gewisse Prozentzahl der Untersuchten liegen. Wenn man einen Bereich sucht, in dem 60% der Untersuchten liegen, dann liegen 20% unterhalb der unteren Grenze und 20% oberhalb der oberen Grenze. In welchem Bereich liegen nun 60% der Männer zwischen 20 und 25 Jahren?
InvNormCD(0.2,10,180)=171,6 und InvNormCD(0.8,10,180)=188,4
Demnach liegen im Bereich von 1,716 m und 1,884 m mind. 60% der Männer.
NormCD(171,6,188,4,10,180)=0,599≈0,60
Sigma-Regeln
Ist die Standardabweichung größer als 3, so ist die sogenannte Laplace-Bedingung erfüllt und man kann die sogenannte σ-Regel anwenden. Man kann hierbei davon ausgehen, dass ein gewisser fester Prozentsatz von Untersuchten in einem gewissen Radius um den Erwartungswert liegt. In der σ-Umgebung liegen 68,3 %, in der 2σ-Umgebung liegen sogar schon 95,4%. Diese Werte kann man der folgenden Tabelle entnehmen.
|
Intervall |
σ |
2σ |
3σ |
0,6745σ |
0,842σ |
1,036σ |
1,282σ |
1,645σ |
1,960σ |
2,576σ |
|
Wahrscheinlichkeit |
68,3% |
95,4% |
99,7% |
50% |
60% |
70% |
80% |
90% |
95% |
99% |
Mit Hilfe dieser Regel lassen sich auch ganz schnell diese Bereiche um den Erwartungswert berechnen, in denen eine bestimmte Prozentzahl von Ergebnissen liegen.
Bei 60% muss man also die 0,842σ–Umgebung bestimmen. Da im obigen Beispiel σ=10 ist, ist der Radius um den Erwartungswert 8,42. Somit ergibt sich das Intervall:
[180-8,42|180+8,42]= [171,58|188,42]
In diesem Intervall liegen 60% der Ergebnisse.