6. Integralrechnung
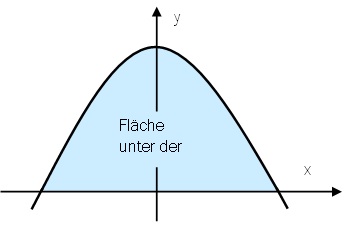
Die Integralrechnung ist eine Art Flächenberechnung. Dabei handelt es sich um den Flächeninhalt unter krummlinigen Kurven von Funktionen. Solche Flächen können nicht einfach mit Länge mal Breite berechnet werden.
Das Problem solcher Flächenberechnung ist schon sehr alt und wurde bereits von ARCHIMEDES (287 – 212 v.u.Z.) untersucht. ARCHIMEDES hat z.B. berechnet, wie groß der Flächeninhalt unter einer Parabel ist.
Eine grundlegende Idee für diese Flächenberechnung ist folgende: Man versucht, eine „Kurvenfläche“ mit solchen Flächen auszufüllen, die man leicht berechnen kann. Das sind vor allem Rechteck- und Dreieickflächen. Dann summiert man diese Teilflächen und erhält die Gesamtfläche.
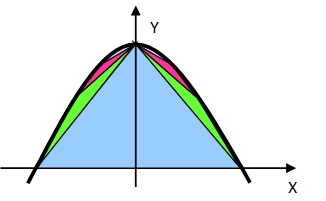
Theoretisch kann man mit allerkleinsten Dreiecken die Parabelfläche ganz ausfüllen. Allerdings nur, wenn man das unendlich fortsetzt, denn es zeigt sich, dass immer noch Platz freibleibt, so klein das Dreieck auch wird. Man bekommt mit dieser Methode doch schon recht genaue Ergebnisse.
Man sieht, dass statt der Dreiecke auch Rechtecke oder Trapeze oder Kombinationen solcher Figuren genommen werden können. Die Flächen lassen sich leicht berechnen und müssen nur summiert werden. Das Ergebnis ist aber immer nur hinreichend genau.
6.1. Ober- und Untersummen
Bei einer linearen Funktion durch den Ursprung ist die Berechnung der Fläche zwischen 0 und b noch sehr einfach. Hierfür hat man eine Flächenformel für Dreiecke.
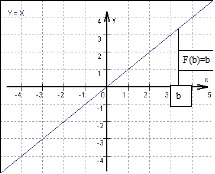
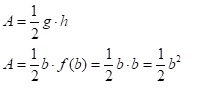
Bei einer Parabel ist die Berechnung schon komplizierter. Hier versucht man sich durch Rechtecke unterhalb der Funktion dem Ergebnis anzunähern, indem man die Anzahl der Rechtecke erhöht, dabei aber alle Rechtecke die gleiche Breite haben. Diese Verfahren nennt man in der Mathematik „die Untersumme der Rechtecksflächen“.
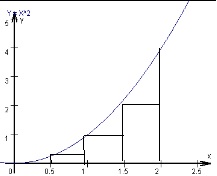
Man könnte aber auch die Rechtecke oberhalb der Funktion bilden, dann nennt man dies die „Obersumme der Rechtecksflächen“.
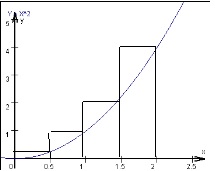
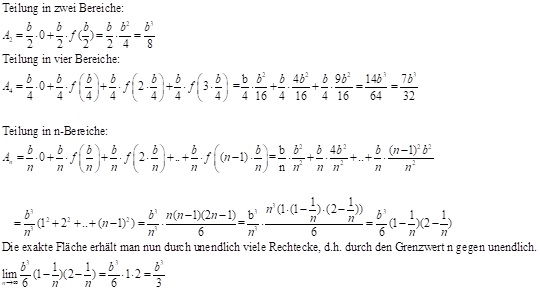
Vielleicht erkennt man bei den Potenzfunktionen schon eine Gesetzmäßigkeit.
f(x) = x hat als Fläche b2/2 – f(x) = x2 hat als Fläche b3/3
Wir vermuten dass f(x) = x3 die Fläche b4/4 hat und allgemein f(x) = xn die Fläche b(n+1)/(n+1) hat.
Schreibt man diese Flächen nicht mit b als Variable sondern als Funktion von x, d.h. die Grenze zur Flächenberechnung ist die Funktionsvariable x, so spricht man von der Integralfunktion oder Stammfunktion F(x).
Die oben erkannte Gesetzmäßigkeit lässt sich als sogenannte Potenzregel beim Integrieren formulieren.
Potenzregel:
Die Funktion f(x)=xn ist integrierbar und hat als Stammfunktion die
Funktion F(x) = [xn+1/(n+1)].
Man erkennt, dass man bei Integrieren den Exponenten um 1 erhöht und durch diesen teilt. Beim Ableiten wird der Exponent um 1 kleiner und man multipliziert mit dem alten Exponenten. Somit vermutet man, dass das Integrieren die Umkehrung des Differenzierens ist.
Eine Funktion F(x), die abgeleitet wieder die Ausgangsfunktion f(x) ergibt, nennt man allgemein Stammfunktion von f(x). Da das Differenzieren auch Ableiten genannt wird, nennt man Integrieren auch Aufleiten.
Die berechnete Fläche beginnt aber dabei immer bei x = 0. Möchte man aber eine Fläche von x=a bis x=b (A1) berechnen, so berechnet man zunächst die ganze Fläche von x= 0 bis x = b (A1 + A2) und subtrahiert dann das 1. Flächenstück von 0 bis a (A2). Somit benötigt man bei der Flächenberechnung bzw. Integration eine obere Grenze b und eine untere Grenze a.
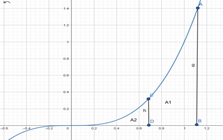
Zur Berechnung der Fläche zwischen der Funktion f(x) und der x-Achse im Intervall von a bis b benötigt man eine Stammfunktion, in der man zuerst die obere Grenze einsetzt und dann die untere Grenze einsetzt und diese von der großen Fläche abzieht. Diesen Zusammenhang kann man im Hauptsatz der Differential- und Integralrechnung nachlesen.
Hauptsatz der Differential-und Integralrechnung:
- Ableiten und Integrieren sind Umkehrungen voneinander, d.h. leitet man F(x) ab, so erhält man die Ausgangsfunktion f(x) – integriert man f(x), so erhält man F(x).
- Hat man eine Stammfunktion F(x) zu f(x) bestimmt, so wird das Integral von f(x) (die Größe des Flächenstücks zwischen Funktion und x-Achse im Intervall von a bis b) folgendermaßen berechnet:
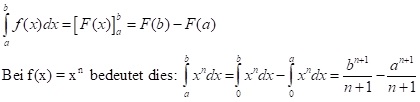
a ist dabei die untere Grenze und b ist die obere Grenze der Flächenberechnung. Diese Grenzen braucht man nur in die sogenannte Stammfunktion einsetzen.
6.2. Rechenregeln zur Integralrechnung
Bei ganzrationalen Funktionen ist der Funktionsterm zusammengesetzt aus Summen oder Differenzen von Potenzen von x, die aber auch noch mit einem Faktor multipliziert werden können.
Beispiel: f(x) = 3x3 + 4x2 – 6x +5
Diese Regeln kann man auch wieder auf die Regeln der Differentialrechnung beziehen. Auch hier bleiben Faktoren einfach stehen und Summen und Differenzen werden einzeln integriert oder aufgeleitet. Dies besagen die Faktorregel und die Summen- und Differenzregel.
Faktorregel:
Ist g(x) integrierbar mit der Stammfunktion G(x) so ist auch f(x)=a×g(x) integrierbar und es gilt:
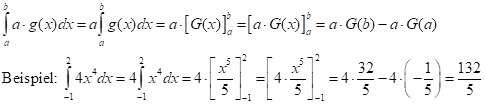
Summen- und Differenzregel:
Sind g(x) und h(x) integrierbar mit den Stammfunktionen G(x) und H(x) so ist auch
f(x)=g(x) ± h(x) integrierbar und es gilt:
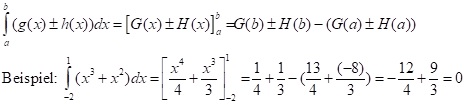
Das Beispiel zeigt, dass es positive und negative Integrale gibt, je nachdem ob f(x) oberhalb (+) oder unterhalb (-) der x-Achse verläuft. So können sich positive und negative Anteile gegenseitig aufheben, was man bei einer Flächenberechnung berücksichtigen muss, da Flächen nur positiv sein können.
Mit Hilfe der Potenzregel lassen sich nicht nur Stammfunktionen von Polynomen leicht finden, man kann auch Stammfunktionen von Wurzeln oder Potenzen von x finden, die im Nenner stehen, da man diese Funktionen als Potenzen von x schreiben kann. Hier ein paar Beispiele:
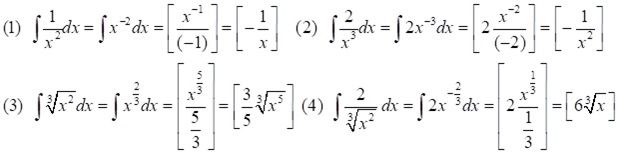
Aufgabe 1: Berechne zu folgenden Funktionen eine Stammfunktion.
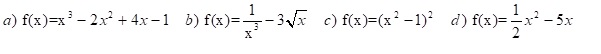
Aufgabe 2: Berechne folgende Integrale.
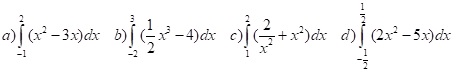
Aufgabe 3: Berechne den Parameter t so, dass die angegebene Gleichung erfüllt ist.
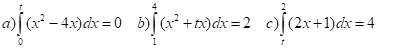
6.3. Flächenberechnung
Die Integralrechnung beschäftigt sich mit der Berechnung von Flächeninhalten.
Zunächst versuchen wir den Flächeninhalt zwischen einem Funktionsgraphen und der x-Achse und danach den Flächeninhalt zwischen zwei Funktionsgraphen zu berechnen.
- a) Fläche zwischen f(x) und der x-Achse
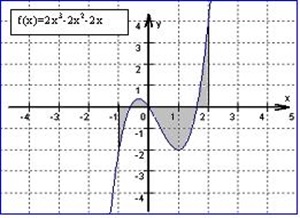
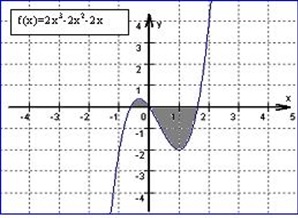
Eine Funktion kann mehrere Nullstellen haben und die eingeschlossene Fläche kann über oder unter der x-Achse liegen. Liegt das Flächenstück oberhalb der x-Achse, so ist das Integral positiv. Liegt es aber unterhalb der x-Achse, so ist das Integral negativ und muss zur Berechnung der Gesamtfläche positiv gemacht werden.
Man sieht nicht sofort, wo die Funktion oberhalb oder unterhalb der x-Achse liegt. Deshalb muss man die Integrale von Nullstelle bis Nullstelle einzeln berechnen und positiv machen. Auch können noch seitliche Intervallgrenzen (obere und untere Grenze) angegeben werden, die auch noch eine seitliche Begrenzung der Fläche darstellen.
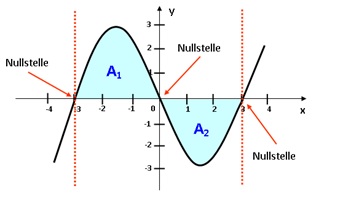
Bei der Integralrechnung gibt es keine „negativen“ Flächen, es wird immer der absolute Betrag des Ergebnisses genommen.
Es kann nicht über Nullstellen hinweg integriert werden. Wenn die Funktion Nullstellen hat, werden die einzelnen Teilflächen jede für sich integriert. Die Teilflächen werden zur Gesamt-Integral-Fläche summiert. Mit der Betragsfunktion macht man jedes Integral bei der Berechnung positiv.
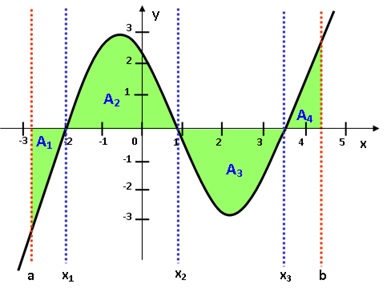
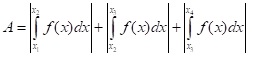
Ach kann man Intervallgrenzen angeben, die zwischen den Nullstellen oder außerhalb dieser Bereiche liegen kann. Dann nimmt man nur die Nullstellen, die innerhalb des Intervalls liegen. Innerhalb des Intervalls werden die Teilflächen integriert und zur Gesamtfläche summiert.
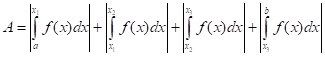
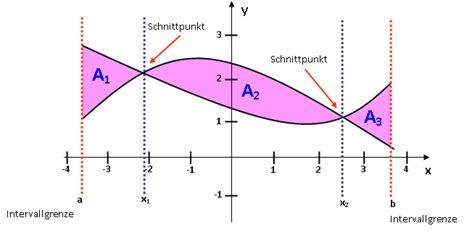
- b) Fläche zwischen zwei Funktionen
Ähnlich wie bei der Fläche zwischen f(x) und der x-Achse muss man hier aber zur Berechnung der Fläche, die von zwei Graphen eingeschlossen wird, die Schnittpunkte statt den Nullstellen betrachten und die Integrale hier trennen. Auch hier darf nicht über die Schnittpunkte hinweg integriert werden. Dabei spielt keine Rolle, ob die Fläche nun oberhalb oder unterhalb der x-Achse liegt, da man hierbei die Differenzfunktion f(x) – g(x) integriert, die von Schnittstelle zu Schnittstelle immer im positiven oder im negativen Bereich liegt.
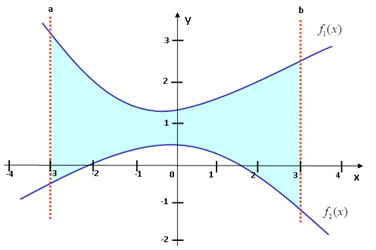
Bei Funktionen, deren Graphen sich nicht schneiden, wird die Fläche zwischen den Graphen so berechnet:
6.1. Anwendungsaufgaben
Aufgabe1:
Gegeben ist die Funktion f mit ![]()
Ein Teil des Graphen von f ist für 0 ≤ t ≤15
zeigt nebenstehende Skizze.
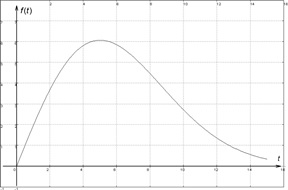
- Für 0 ≤ t ≤15 beschreibt f(t) modellhaft die momentane Sauerstoffproduktion einer Buche an einem Sommertag mit 15 Stunden Sonnenscheindauer ab dem Sonnenaufgang (t =0), wobei man t in Stunden und f(t) in m3 pro Stunde angibt. Bestimmen Sie mit Hilfe eines geeigneten Integrationsverfahrens eine Stammfunktion von f.
(Zur Kontrolle und weiteren Verwendung: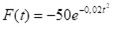 )
) - Berechnen Sie den Inhalt der Fläche, die von der t-Achse, dem Graphen von f und der Geraden mit t =10 eingeschlossen wird.
- Interpretieren Sie den bei b) berechneten Flächeninhalt in diesem Sachzusammenhang. Bestimmen Sie, wie viele Sonnenstunden vergangen sind, bis die Buche insgesamt 20 m3Sauerstoff produziert hat.
Aufgabe2: Gegeben ist die Funktion f mit ![]()
Ein Teil des Graphen von f ist für 0 ≤ t ≤12
zeigt nebenstehende Skizze.
Für 0 ≤ t ≤12 beschreibt f(t) modellhaft die momentane Sauerstoffproduktion einer Buche an einem Sommertag mit 12 Stunden Sonnenscheindauer ab dem Sonnenaufgang (t =0), wobei man t in Stunden und f(t) in m3 pro Stunde angibt.
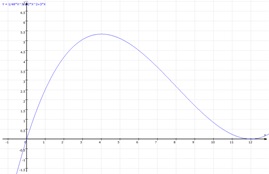
- Beschreibe den Funktionsverlauf im Sachzusammenhang und beantworte folgende Fragen:
– Wann ist die Sauerstoffproduktion am größten?
– Wann ist die Zunahme der Produktion am größten und wann ist die Abnahme der Produktion am größten?
– Wann wird kein Sauerstoff produziert? - Berechne den Inhalt der Fläche, die von der t-Achse und dem Graphen von f eingeschlossen wird. Was hast du damit ausgerechnet in Bezug zur Sauerstoffproduktion?
- Bestimme, wie viele Sonnenstunden vergehen müssen, damit die Buche insgesamt 10 m3Sauerstoff produziert hat.
- Wie viel Sauerstoff produziert die Buche in den ersten 6 Stunden durchschnittlich pro Stunde?
Aufgabe 3:
Um die Wasserstände eines Flusses vorherzusagen, kann man versuchen, die Durchflussgeschwindigkeit des Wassers an einer bestimmten Stelle des Flusses mit Hilfe geeigneter Funktionen zu beschreiben. Solche näherungsweise Beschreibungen der Durchflussgeschwindigkeiten seien z.B. gegeben durch die Funktionsschar f mit ![]() .
.
Dabei gibt fa(t) die Durchflussgeschwindigkeit in 106m3/Monat (Millionen Kubikmeter pro Monat) und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage (t =0) an. Die Funktionen f berücksichtigen, dass es sich um einen Fluss handelt, der zeitweise austrocknet.
- Zeige, dass es für t >0 keine negativen Funktionswerte geben kann.
- Bestimme für a =3, wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.
- Berechne für a = 3 die durchschnittliche Wassermenge der ersten 3 Monate und für den Zeitraum von April bis September.
- Betrachten Sie nun zwei verschiedene Funktionen fa1 und fa2 . Bestimmen Sie den Zeitpunkt t0 , zu dem für beide Funktionsannahmen (seit t =0 ) genau gleich viel Wasser durch den Fluss geflossen wäre.
Aufgabe 4: Zum Zeitpunkt t = 0 erfolgte die Einnahme eines Medikamentes. Gemessen wurde die Wirkstoffmenge in der Leber in mg. Zu den Messpunkten wurde eine Ausgleichkurve mit der Gleichung w(t) = t‧(t+5)‧e -t gezeichnet. Im Graphen sind ein Hoch- und ein Wendpunkt zu sehen.
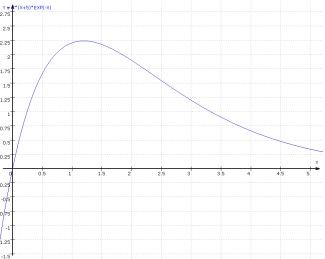
- Für die medizinische Wirksamkeit eines Medikamentes kommt es neben der Menge des Wirkstoffes auch auf die Zeit an, in der der Wirkstoff für den Körper zur Verfügung steht. Das Produkt aus Menge und Zeit wird „Wirksamkeit“ genannt. Zeigen Sie, dass
W(t) = -(t2 +7t + 7)‧e –t eine Stammfunktion zu w(t) = t‧(t+5)‧e -t ist und berechnen Sie die Wirksamkeit der ersten drei Stunden für diese Funktion. - Gebe eine Formel für die Wirksamkeit für einen bel. Zeitpunkt nach der Einnahme an. Wächst die Wirksamkeit immer weiter oder strebt dieser Wert gegen eine feste Zahl?
- Berechne die Wirksamkeit des Medikamentes für volle Stundenintervalle. Das Medikament muss wieder eingenommen werden, wenn die Wirksamkeit unter 0,5 mg/h liegt. Wann muss man das Medikament wieder einnehmen?