1.1. Mathematische Beschreibung von Abhängigkeiten
Die Mathematik beschäftigt sich in diesem Bereich Abhängigkeiten mit Hilfe von Funktionen zu beschreiben. Ein Sachverhalt ist abhängig von einer Variablen, z.B.
- Wir betrachten alle Geraden mit negativer Steigung m, die durch den Punkt P(2|1) gehen. Sie bilden mit den Koordinatenachsen ein rechtwinkliges Dreieck: Fläche A in Abhängigkeit der Steigung m: A(m) = 2 – 2m – 1 / 2m
- Sparguthaben K in Abhängigkeit der Zeit t bei 6%-iger Verzinsung: K(t) = K0 • 1,06 t
(wobei 1 Zeitschritt 1 Jahr, Anfangskapital) z.B. = 1000, dann ist K(t) = 1000 •1,06 t - Breite y eines Rechtecks mit Umfang 20 in Abhängigkeit der Länge x: y(x) = 10 -x
- Fläche A eines Rechtecks mit Umfang 20 in Abhängigkeit der Länge x: y(x) = 10x – x 2
1.2. Der Begriff „Funktion“
Eine Funktion f ist eine Vorschrift, die jeder reellen Zahl aus einer Definitionsmenge genau eine reelle Zahl zuordnet.
Schreibweise: f : x → f(x) „x wird abgebildet auf f(x)“
Bezeichnungen:
– f (X0 ) „Funktionswert von X0“
– Df „Definitionsmenge der Funktion f“
– Wf „Wertemenge der Funktion f“
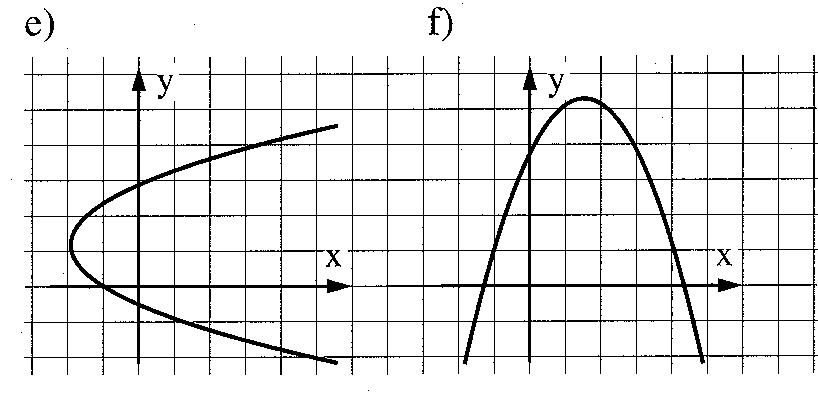
Beispiel Funktion/keine Funktion:
Das Schaubild von e) ist keine Funktion, weil einem x-Wert mehrere Funktionswerte zugeordnet sind.
Bei einer Funktion muss ja jeder reellen Zahl aus der Definitionsmenge genau eine reelle Zahl zuordnet sein (s.o. Kasten).
Bei f) dagegen ist diese Forderung erfüllt. Schaubild f) ist eine Funktion.
Bestimmung der maximal möglichen Definitionsmenge:
(d.h.: der Nenner darf nicht Null sein, unter einer Wurzel darf nichts Negatives stehen…)
Zahlenmengen haben folgende Schreibweisen:
ℕ – natürliche Zahlen {1, 2, 3, …}
ℤ – ganze Zahlen
ℚ – rationale Zahlen (Bruchzahlen)
ℝ – reelle Zahlen (enthält auch die Zahlen, die man nicht als Bruch schreiben kann z.B. ℼ, √2, e (Eulerische Zahl), …
f : x → 3x + 5; D = ℝ (d.h. Definitionsmenge sind alle reellen Zahlen)
g: x → 1/(x2 -3x +2) D = ℝ \ {1; 2} (d.h. „alle reellen Zahlen ohne die 1 und die 2“)
k: x → √(x + 5) D = {x ϵ ℝ |x ≥ -5} (d.h. alle Zahlen x mit der Eigenschaft: x ≥ -5)
j: x →1/√(x + 5) D = { x ϵ ℝ |x > -5} (d.h. alle Zahlen x mit der Eigenschaft: x > -5)
Definitionsmengen kann man auch in Intervallschreibweise angeben.
Eine eckige Klammer schließt die Intervallgrenzen mit ein, runde Klammer nicht.
Beispiele: [ 4 ; 8 ] ist das abgeschlossene Intervall von 4 bis 8, d.h. { x ϵ ℝ | 4 ≤ x ≤ 8 }
( 4 ; 8 ) ist das offene Intervall von 4 bis 8, d.h. { x ϵ ℝ | 4 < x < 8 }
[ 4 ; 8 ) ist das halboffene Intervall von 4 bis 8, d.h. { x ϵ ℝ | 4 ≤ x <8 }
Das Zeichen bedeutet „Unendlich“ bzw. – bedeutet – Unendlich.
D = { x ϵ ℝ |x ≥ -5} kann man auch damit auch so angeben: D = [5 ; + )
1.3. Zusammenstellung bekannter Funktionen
1.3.1. Lineare Funktionen
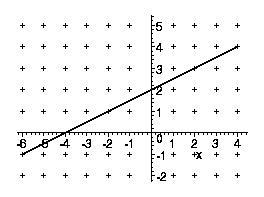
Allg. Form f: x →ax + b D = ℝ
Schaubild: Gerade mit Steigung a, und
y-Achsenabschnitt b
Beispiel: f(x) = 0,5x + 2
Wo liegt die Nullstelle dieser Funktion?
0,5x + 2 = 0 ↔ x = – 4
1.3.2. Quadratische Funktion
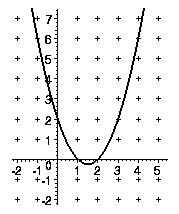
Allg. Form f(x) = ax2 + bx + c
Schaubild: Parabel D = ℝ
Beispiel: f(x) = x2 – 3x + 2
Wo liegen hier die Nullstellen?
x2 – 3x + 2 = 0
Lösung mit p,q-Formel x1/2 = – p/2 ± √(p/2)2-q
→x1 = 1; x2 = 2
1.3.3. Wurzelfunktionen
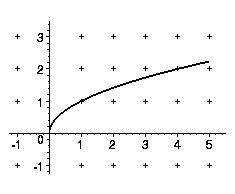
f(x) = √x
Schaubild:
einastige rechtsgeöffnete Parabel
D = [ 0 ; + ∞ )
1.3.4. Trigonometrische Funktionen
Dazu gehört die Sinus-, die Kosinus-
(und die Tangensfunktion)
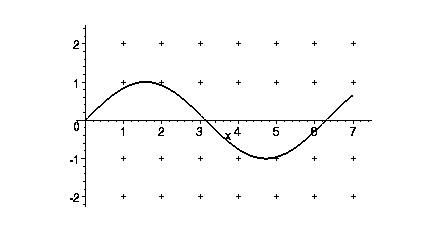
Grundform: f(x) = sin(x)
D = ℝ
W = [ -1 | +1 ]
Nullstellen bei … -ℼ; 0; ℼ; 2ℼ; 3ℼ …
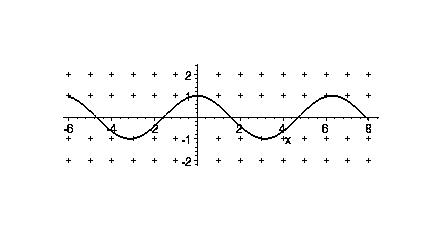
Grundform: f(x) = cos(x)
D = ℝ
W = [ -1 | +1 ]
Nullstellen bei … ℼ/2; 3ℼ/2; 5ℼ/2…
1.3.5. Betragsfunktionen
Die Betragsfunktion f(x) = |x| macht alle Funktionswerte positiv.
1.3.6. Ganzrationale Funktionen
Alle Funktionen mit Potenzen von x, d.h. allgemein
f(x) = anxn + an-1xn-1 + an-2xn-2 + …+ a1x + a0
wobei an ≠ 0 sein muss, heißt ganzrationale Funktion n-ten Grades
Ihr Verhalten für betragsmäßig große Werte von x wird von g(x) = anxn bestimmt, d.h. der höchste Exponent ist für das Grenzwertverhalten im Unendlichen ausschlaggebend.
Sie hat maximal n Nullstellen.
Beispiel:
f(x) = 0,1x4 – 1,3x2 + 1,2x ist eine ganzrationale Funktion 4. Grades.
Ihr Verhalten für betragsmäßig große x-Werte wird von der Potenzfunktion bestimmt, d.h. für geht und für geht .
1.3.7. Weitere Funktionen
– Exponentialfunktionen (hier ist die Funktionsvariable im Exponent)
– Logarithmunsfunktionen (die Umkehrung der Exponentialfunktion, um den Exponenten zu berechnen, d.h. man benutzt sie, wenn der Exponent gesucht ist)