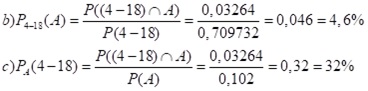4. Bedingte Wahrscheinlichkeit
Häufig werden zwei unterschiedliche Merkmale A und B gemeinsam untersucht. Die Wahrscheinlichkeit, dass Merkmal A und Merkmal B eintritt berechnet man durch Multiplikation der beiden Wahrscheinlichkeiten, d.h. P(A∩B) = P(A) ‧ P(B). Nun kann dieses aber auch so betrachten, dass schon das 1. Merkmal bekannt ist, dann ändert sich die Wahrscheinlichkeit für das 2. Merkmal.
Man sagt: Unter der Bedingung, dass A eingetreten ist, mit welcher Wahrscheinlichkeit tritt dann B ein? Dieses nennt man die bedingte Wahrscheinlichkeit PA(B).
4.1 Bedingte Wahrscheinlichkeit im Baumdiagramm
Wie berechnet man diese „bedingte Wahrscheinlichkeit“? Dazu schauen wir uns einmal ein Baumdiagramm an mit jeweils zwei Ausgängen A und nicht A bzw. B und nicht B.
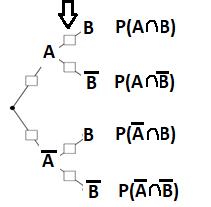
Die bedingte Wahrscheinlichkeit PA(B) ist die Wahrscheinlichkeit, die dort steht, wo der Pfeil hinzeigt, da schon A eingetreten ist und nun die Wahrscheinlichkeit für B berechnet werden muss.
Da die Wahrscheinlichkeiten multipliziert werden, gilt:
P(A) ‧ PA(B) = P(A∩B) und somit für die bedingte Wahrscheinlichkeit folgende Formel gilt:
PA(B) = P(A∩B)/ P(A)
Beispiel:
A: Die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person positiv getestet wurde (ob sie die Krankheit hat oder nicht) beträgt 20%.
A∩B: Die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person eine Krankheit hat und positiv getestet wurde beträgt 15%.
Berechne die Wahrscheinlichkeit, dass eine positiv getestete Person die Krankheit hat.
Dies ist die Bedingte Wahrscheinlichkeit PA(B) = P(A∩B)/ P(A) = 0,15/0,2 = 0,75
D.h. unter der Bedingung, dass eine Person positiv getestet wurde, ist sie mit einer Wahrscheinlichkeit von 75% wirklich an dieser Krankheit erkrankt. 75% ist damit der Anteil der Erkrankten an den positiv getesteten.
4.2 Bedingte Wahrscheinlichkeit mit der Vierfeldertafel
Hilfreich zur Berechnung der bedingten Wahrscheinlichkeit ist die sogenannte Vierfeldertafel, die mit Zeilen- und Spaltensummen vervollständigt wird. Oft sind nur Teile der Vierfeldertafel gegeben, die man aber durch logische Überlegungen vollständig ausfüllen kann.
Beispiel: In einer Urne befinden sich 25 Kugeln aus Holz oder Plastik mit den Farben rot oder blau.
Man weiß, dass 8 Kugeln aus Kunststoff sind und von 13 roten Kugeln sind 7 aus Holz.
| Holz | Kunststoff | Gesamt | |
| rot | 7 | 13 | |
| blau | |||
| Gesamt | 8 | 25 |
Diese Tabelle lässt sich dann komplett ausfüllen. Dies Anzahlen lassen sich auch in Wahrscheinlichkeiten angeben.
| Holz | Kunststoff | Gesamt | |
| rot | 7 (0,28) | 6 (0,24) | 13 (0,52) |
| blau | 10 (0,4) | 2 (0,08) | 12 (0,48) |
| Gesamt | 17 (0,68) | 8 (0,32) | 25 Kugeln (1) |
Die Wahrscheinlichkeit, eine blaue Holzkugel zu ziehen, ist 40%.
Die Wahrscheinlichkeit, eine Kunststoffkugel zu ziehen, ist 32%.
Die Wahrscheinlichkeit, eine blaue Kugel zu ziehen, ist 48%. …
Für die bedingten Wahrscheinlichkeiten, muss man dann die Werte in die Formel einsetzen.
Wie groß ist die Wahrscheinlichkeit eine rote Kugel zu ziehen, wenn man weiß, dass sie aus Holz ist?
PH(r)=P(H∩r)/P(H)=0,28/0,68=0,4118=41,18%.
Man zieht eine blaue Kugel. Wie groß ist die Wahrscheinlichkeit, dass sie aus Kunststoff ist?
Pb(K)=P(K∩b)/P(b)=0,08/0,48=0,1667=16,67%
Mit Hilfe der Vierfeldertafel kann man auch ganz leicht ein Baumdiagramm erstellen auch in umgekehrter Reihenfolge, da man entweder mit der Farbe oder mit dem Material beginnen kann.
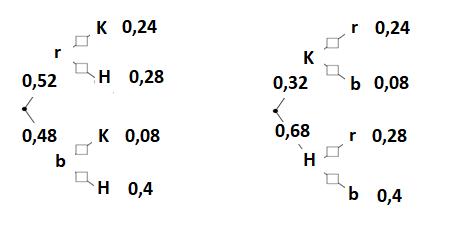
Auch hier müssen die bedingten Wahrscheinlichkeiten durch Division berechnet werden.
Falls man noch mehr Eigenschaften eines Merkmals hat, so kann die Vierfeldertafel natürlich auch noch beliebig erweitert werden zu einer Tafel mit 2×3=6 Feldern oder 3×3=9 Feldern usw.
4.3 Aufgaben zur bedingten Wahrscheinlichkeit
Aufgabe 1:
Die Nutzung des Fahrrads als regelmäßiges Verkehrsmittel auf dem Weg zur Arbeit hängt unter anderem von der Ortsgröße ab.
| Ortsgröße | Anteil der Personen, die in einem Ort der angegebenen Ortsgröße leben | davon regelmäßige Nutzung des |
| unter 20 000 Einwohner | 40,4 % | 37 % |
| 20 000 bis 100 000 Einwohner | 29,0 % | 42 % |
| über 100 000 Einwohner | 30,6 % | 43% |
- Bestimme die Wahrscheinlichkeit dafür, dass eine aus der Bevölkerung zufällig ausgewählte Person aus einer Stadt mit mehr als 100 000 Einwohnern kommt und ihr Fahrrad regelmäßig als Verkehrsmittel nutzt.
- Bestimme die Wahrscheinlichkeit dafür, dass eine aus der Bevölkerung zufällig ausgewählte Person, die angibt, ihr Fahrrad nicht regelmäßig als Verkehrsmittel zu nutzen, aus einer Großstadt mit mehr als 100 000 Einwohnern kommt.
Lösung:

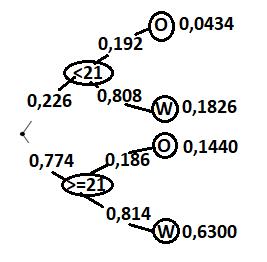
Aufgabe 2: 22,6 % der Bevölkerung in Deutschland ist unter 21 Jahre alt. 80,8 % dieser jüngeren Personen leben in Westdeutschland. 81,4 % der Personen, die 21 Jahre oder älter sind, wohnen in Westdeutschland.
- Fertige ein komplettes Baumdiagramm an (Zuerst Alter dann Ost/West).
- Eine Person aus Ostdeutschland wird zufällig ausgewählt. Mit welcher Wahrscheinlichkeit ist sie 21 Jahre und älter?
- Eine Person, die 21 Jahre ist oder älter, wird zufällig ausgewählt. Mit welcher Wahrscheinlichkeit ist sie aus Ostdeutschland?
Lösung:
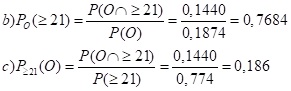
Aufgabe 3: Von 30 Schülern haben 15 Schüler den Mathematik Leistungskurs, 12 Schüler den Deutsch Leistungskurs und 7 haben beide Leistungskurse gewählt. Ein Schüler wird zufällig ausgewählt.
- Wie groß ist die Wahrscheinlichkeit dafür, dass der Schüler Mathematik LK und Deutsch LK gewählt hat.
- Wie groß ist die Wahrscheinlichkeit dafür, dass der Schüler weder Mathematik LK noch Deutsch LK gewählt hat.
- Ein Schülermit Mathematik LK wird ausgewählt. Mit welcher Wahrscheinlichkeit hat er keinen Deutsch LK?
Lösung:
| Deutsch LK | kein Deutsch LK | Gesamt | |
| Mathematik LK | 7 | 8 | 15 |
| Kein Mathematik LK | 5 | 10 | 15 |
| Gesamt | 12 | 18 | 30 |
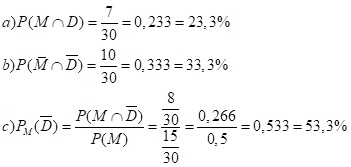
Aufgabe 4: Im vergangenen Jahr hat man 390 000 Unfälle mit Personenschäden registriert, wovon 10,2 % durch Alkohol verursacht wurden. 24,6 % der Unfälle ohne Alkohol fanden zwischen 18 Uhr und 4 Uhr morgens statt. 68,0 % der Alkoholunfälle fielen auch in diesen Zeitraum.
- Fertige eine Vierfeldertafel an.
- Wie groß ist die Wahrscheinlichkeit, dass ein Unfall unter Alkoholeinwirkung geschah, wenn bekannt ist, dass er zwischen 4 Uhr morgens und 18 Uhr stattfand?
- Wie groß ist die Wahrscheinlichkeit, dass ein Unfall zwischen 4 Uhr morgens und 18 Uhr stattfand, wenn bekannt ist, dass Alkohol im Spiel war?
Lösung:
a)
| Von 4 bis 18 Uhr | Von 18 bis 4 Uhr | Gesamt | |
| Mit Alkohol | 0,03264 | 0,102*0,68=0,06936 | 0,102 |
| Ohne Alkohol | 0,677092 | o,898*0,246=0,220908 | 0,898 |
| Gesamt | 0,709732 | 0,290268 | 1 |