3. Ebenen
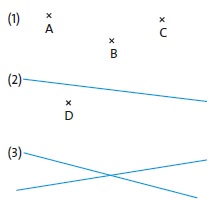
Ebenen im Raum sind Flächen, die in allen Richtungen der Ebene unbegrenzt sind. Sie können überall im Koordinatensystem liegen. Die Lage einer Ebene ist eindeutig durch drei Punkte festgelegt (1), die nicht auf einer gemeinsamen Geraden liegen und deshalb ein Dreieck bilden. Alternativ ist eine Ebene auch durch eine Gerade und einen Punkt, der nicht auf der Geraden liegt (2), oder durch zwei verschiedene Geraden eindeutig bestimmt (3).
Ebenen können unterschiedliche Lagebeziehungen zueinander oder anderen Objekten (Punkte, Geraden, Kugeln, …) haben.
Eine Ebene im 3-dimensionalen Raum hinterlässt im Koordinatensystem eine Spur, die als Schnittmengen der Ebene mit den Koordinatenachsen bzw. Ebenen des Koordinatensystems. Je zwei Koordinatenachsen spannen eine Koordinatenachsenebene auf. Die Schnittpunkte einer Ebene mit den Koordinatenachsen nennt man Spurpunkte, je zwei Spurpunkte definieren eine Spurgerade, die in einer Koordinatenachsenebene liegt.
3.1. Ebenen in Parameterform
Wie bei Geraden kann man eine Ebene auch mit Vektoren und Parametern beschreiben. Man erreicht jeden beliebigen Punkt der Ebene, in dem man mit einem Ortsvektor zu einem Punkt der Ebene gelangt. Von dort aus geht man dann nicht nur in eine Richtung, sondern in zwei verschiedenen Richtungen. Vervielfacht man dann diese Richtungsvektoren, so kann man zu jedem beliebigen Punkt der Ebene gelangen (siehe Abbildung).
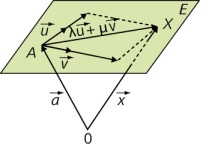
So braucht man zur Beschreibung einer Geraden entweder 3 Punkte, 2 Punkte und einen Richtungsvektor oder 1 Punkt und zwei Richtungsvektoren. Hat man keine zwei Richtungsvektoren gegeben, so muss man aus den Punkten mit einem Verbindungsvektor Richtungsvektoren berechnen. Verlaufen diese Richtungsvektoren in unterschiedliche Richtungen, so erzeugen diese eine Ebene und man kann die Ebene in Parameterform bestimmen.
Die Ebenengleichung in Parameterform lautet:
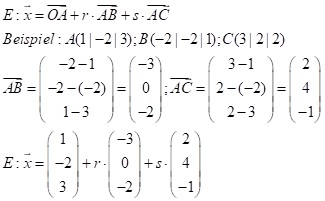
Durch Einsetzen von r und s in die Ebenengleichung erhält man jeden beliebigen Punkt x der Ebene E.
Möchte man prüfen, ob ein Punkt P in der Ebene liegt, so muss man den Ortsvektor zum Punkt P für den Vektor x in die Ebenengleichung einsetzen. Dies ist die Punktprobe für Ebenen.
Aufgabe: Eine Ebene E ist gegeben durch die Punkte A(-1|1|1), B(-3|-2|2) und C(2|1|-1).
- Bestimme eine Ebenengleichung in Parameterform, in der die drei Punkte A, B und C liegen.
- Gebe weitere 4 Punkte der Ebene an
- Prüfe, ob die Punkte D(4|-3|3) oder E(3|-2|6) in der Ebene E liegen.
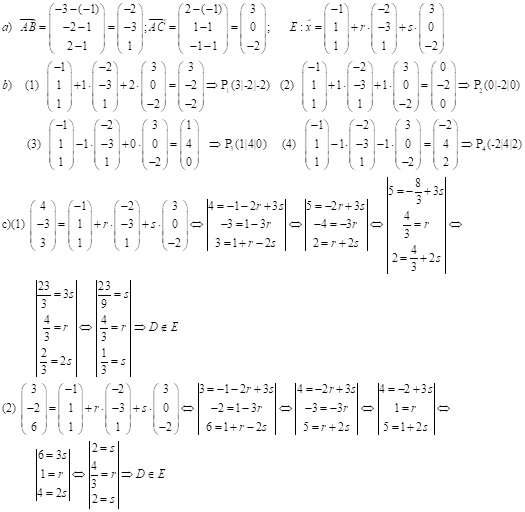
3.2. Ebenen in Normalform und in Koordinatengleichung
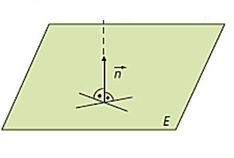
Statt die Richtung der Ebene mit Hilfe von zwei Richtungsvektoren anzugeben, kann man die Richtung auch durch einen senkrecht zur Ebene verlaufenden Vektor festlegen. Diesen Vektor nennt man Normalenvektor (siehe Abbildung).
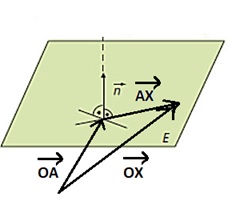
Durch die Eigenschaft, dass der Normalenvektor senkrecht zur Ebene als auch zu jedem Vektor in der Ebene verläuft, erhält man die Normalenform oder Normalengleichung der Ebene, da das Skalarprodukt des Normalenvektors und eines Vektors in der Ebene Null sein muss. Betrachtet man folgende Abbildung, so kann man mit den verwendeten Vektoren eine Gleichung aufstellen.

Aufgabe 1: Gegeben sind drei Punkte der Ebene E mit A(-2|1|-1), B(2|-1|1) und C(3|-3|2).
- Bestimme eine Parametergleichung der Ebene E.
- Berechne eine Normalform von E und eine Koordinatengleichung von E.
- Liegt der Punkt P(-2|3|4) in der Ebene E?
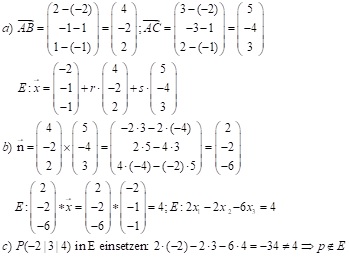
Aufgabe 2: Gegeben ist die Ebene E in der Koordinatengleichung E:2x1+x2-2x3=5.
- Gebe den Normalenvektor an.
- Berechne 3 Punkte, die in der Ebene E liegen.
- Bestimme zu E eine Ebenengleichung in Parameterform.

3.3. Lagebeziehung von Gerade mit einer Ebene
Hierbei gibt es 3 mögliche Lagebeziehungen. Entweder sind Gerade und Ebene parallel oder die Gerade liegt sogar ganz in der Ebene oder sie schneiden sich in einem Punkt. Zu erkennen ist dies an der Anzahl möglicher gemeinsamer Punkte, die man mit Hilfe von Gleichungen berechnen kann.
(1) Die Ebene ist in Parameterform
Hier setzt man Ebene und Gerade gleich und erhält ein Gleichungssystem von 3 Gleichungen mit 3 Variablen. Man erhält dann eine Lösung (Schnittpunkt) oder keine Lösung (parallel) oder unendlich viele Lösungen (g liegt in E).

(2) Ebene in Koordinatengleichung
Hier muss man die Koordinaten der Geradengleichung in E einsetzen. Man erhält eine Gleichung mit einer Variablen – der Parameter der Geradengleichung.
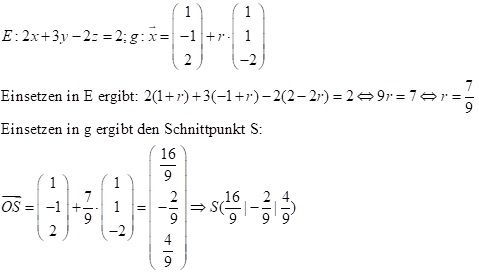
3.4. Lagebeziehungen von Ebenen
Zwei Ebenen können im 3-dimensionalen Raum parallel oder sogar identisch sein oder sie schneiden sich in einer Schnittgeraden.
Um die Parallelität zweier Ebenen zu untersuchen, gibt es mehrere Möglichkeiten. Eine Möglichkeit besteht darin, die Normalenvektoren der beiden Ebenen zu vergleichen. Damit die Ebenen parallel sind, müssen die Normalenvektoren in die gleiche Richtung verlaufen, d.h. Vielfache voneinander sein.
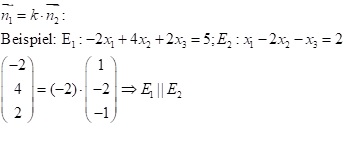
Bei Ebenen in Parameterdarstellung müssen beide Richtungsvektoren der einen Ebene von den beiden Richtungsvektoren der anderen Ebene erzeugt werden.
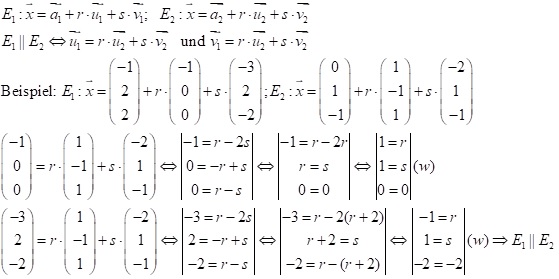
Wenn die Normalenvektoren nicht parallel sind oder die Richtungsvektoren sich nicht erzeugen, dann schneiden sich die Ebenen in einer Geraden.
Ein Beispiel für zwei parallele Ebenen könnte folgendermaßen aussehen:
Ebene 1: x + y + z = 5
Ebene 2: x + y + z = 8
Man kann auch die Schnittpunkte der beiden Ebenen betrachten. Wenn man die Gleichungen der beiden Ebenen gleichsetzt, erhält man:
x + y + z = 5
x + y + z = 8
Addiert man beide Gleichungen, so erhält man 0 = -3, was nicht erfüllt ist. Daher haben die beiden Ebenen keine gemeinsamen Punkte und sind somit parallel.
Schnittgerade berechnen
Wenn zwei Ebenen nicht parallel sind, so schneiden sie sich in einer gemeinsamen Geraden. Diese Schnittgerade kann man auf unterschiedliche Arten berechnen.
(1) Beide Ebenen sind in Koordinatengleichung
Hierbei erhält man ein Gleichungssystem von 2 Gleichungen mit 3 Variablen. Zunächst muss man aus jeder Gleichung eine Variable eliminieren. Dann stellt man jede Gleichung nach einer anderen Variablen um. Die 3. Variable des Gleichungssystems, die meist in beiden Gleichungen noch vorkommt, wird dann als Parameter der Geradengleichung gesetzt. x, y und z sind die drei Koordinaten der Geradengleichung.
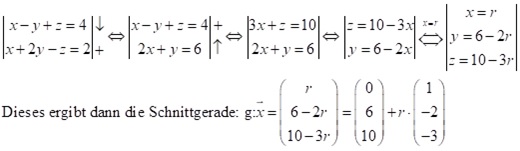
(2) Eine Ebene ist in Koordinatenform und eine ist in Parameterform
Hierbei setzt man die Koordinaten der Parameterform in die Koordinatengleichung ein und stellt diese nach einer Variablen um. Diese wird dann in der Parameterform ersetzt, so dass man nur noch einen Parameter, was dann eine Geradengleichung ergibt.
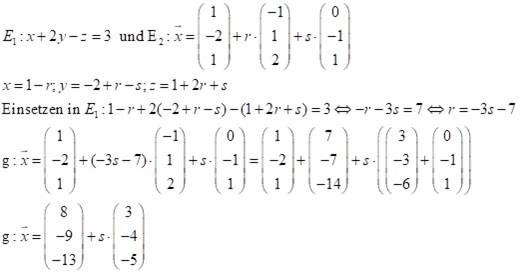
(3) Beide Ebenen sind in Parameterdarstellung
Man setzt beide Ebenen gleich und erhält ein Gleichungssystem mit 3 Gleichungen und 4 Variablen. Dieses Gleichungssystem muss man so bearbeiten, dass eine Gleichung nur noch die Variablen der 1. Ebene enthält und eine Gleichung nur noch die Variablen der 2. Ebenen hat. Dann kann man durch Ersetzen eines Parameters der Ebenengleichung daraus eine Gerade machen, da man dann nur noch einen Parameter hat.
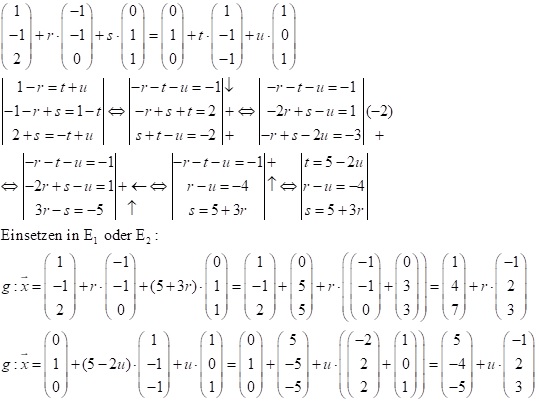
Vor der Berechnung kann man aber auch jeder Ebenendarstellung in eine andere umformen, so dass man dann die einfachere Berechnung nehmen kann.
3.5. Schnittwinkel bei Ebenen
Der Schnittwinkel bei Ebenen lässt sich mit dem Winkel zwischen den Normalenvektoren bestimmen, da sich ja beide Richtungen sich um 90 Grad verändern und somit aber wieder mit dem Schnittwinkel übereinstimmt. Da wir auch hier wieder den spitzen Winkel als Ergebnis nehmen, müssen wir auch hier wieder den Betrag nehmen und das Skalarprodukt im Zähler positiv machen. Bei der Parameterdarstellung bei Ebenen lässt sich kein Schnittwinkel berechnen, da wir je zwei Richtungsvektoren haben.
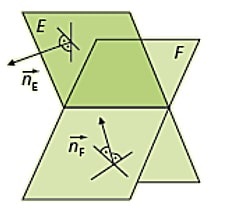
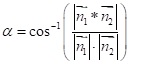
Beim Schnittwinkel zwischen einer Geraden und einer Ebene sieht es etwas anders aus, da der Normalenvektor ja nicht in Richtung der Ebene verläuft. Deshalb muss man hier den Winkel berechnen, in dem man das Ergebnis um 90 Grad versetzt. Dieses macht aber automatisch die Sinusfunktion im Vergleich zur Kosinusfunktion. Deshalb braucht man nur in der Formel den Sinus verwenden.
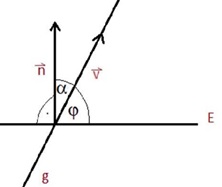
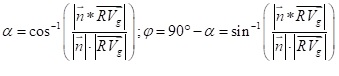
3.6. Abstände bei Ebenen
Bei Ebenen kann man den Abstand eines Punktes zu einer Ebene, den Abstand einer parallelen Geraden zu einer Ebene oder den Abstand zweier paralleler Ebenen untersuchen. Bei einer parallelen Gerade oder auch Ebene ist es aber auch wieder egal, von welchem Punkt man den Abstand berechnet, da der Abstand überall gleich ist. Dies kann man aus der Eigenschaft von Parallelität ableiten. Demnach kann man alle Abstände bei Ebenen mit dem Abstandsproblem von Punkt und Ebene berechnen.
Abstand Punkt und Ebene
Da man bei Ebenen einen Normalenvektor hat, kann man mit diesem senkrechten Vektor den Lotfußpunkt und dann auch den Abstand berechnen. Dazu bilden der Normalenvektor und der Punkt P außerhalb der Ebene eine Hilfsgerade, mit der man dann den Schnittpunkt Q mit der Ebene berechnet. Die Länge der Vektors zwischen P und Q ist dann der Abstand.
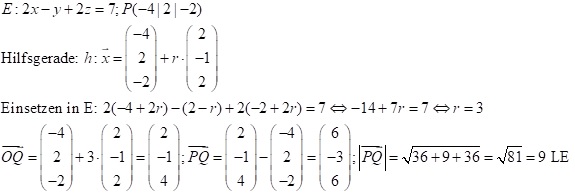
Für den Abstand eines Punktes P zu einer Ebene E gibt es auch eine Abstandsformel:

3.7. Spurpunkte und Spurgeraden
Spurpunkte und Spurgeraden sind die Schnittpunkte mit den Koordinatenachsen bzw. mit den Koordinatenachsenebenen. Je zwei Koordinatenachsen bilden eine Ebene.
(1) Spurgeraden bei Ebenen
Die x- und y-Achse bilden die Koordinatenachsenebene Ex,y: z = 0 .
Die x- und z-Achse bilden die Koordinatenachsenebene Ex,z: y = 0 .
Die y- und z-Achse bilden die Koordinatenachsenebene Ey,z: x = 0 .
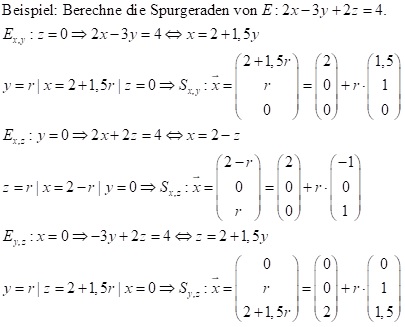
(2) Spurpunkte bei Ebenen
Die Koordinatenachsen haben folgende Gleichungen:

Verbindet man zwei Spurpunkte zu einer Geraden, so kann man auch die Spurgeraden bestimmen.
(3) Spurpunkte bei Geraden
Eine Gerade hinterlässt im Koordinatensystem auch eine Spur. Diese Schnittpunkte mit den Koordinatenachsenebenen nennt man auch Spurpunkte der Geraden.

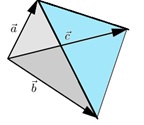
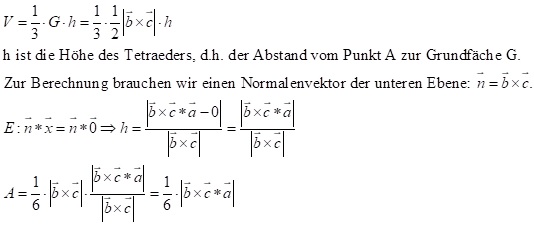
3.8. Volumen eines Tetraeders
Das Volumen V eines Tetraeders, der von drei Vektoren aufgespannt wird, lässt sich mit dem Kreuzprodukt berechnen: