5. Binominalverteilung
5.1 Bernoulli-Experimente
Wir betrachten zunächst ein sogenanntes Bernoulli-Experiment. Bei diesem Zufallsexperiment gibt es nur 2 mögliche Ausgänge (d.h. 2 Elementarereignisse). Das eine nennen wir A und tritt mit der Wahrscheinlichkeit p auf, das andere ist dann nicht A und tritt mit der Wahrscheinlichkeit q=1−p auf. Beispiel:
– Beim Münzwurf gibt es nur zwei Ausgänge Kopf oder Zahl jeweils mit der Wahrscheinlichkeit 0,5.
– Beim Würfeln kann man nur eine Zahl betrachten und sein Gegenereignis. Zum Beispiel die sechs zu würfeln oder keine 6 zu würfeln.
Führt man ein Bernoulli-Experiment n −mal (unabhängig voneinander) durch und betrachtet man die Zufallsvariable X = Anzahl, wie oft A aufgetreten ist, dann ist X binomialverteilt mit den Parametern n und p.
5.2 Genaue Anzahl von Treffern (X=k)
Nun wollen wir eine Formel für die Wahrscheinlichkeit aufstellen, bei einem Bernoulli Versuch mit n Versuchen k Treffer zu erzielen. A soll also k-mal eintreten mit der Wahrscheinlichkeit p und Nicht A soll n-k mal eintreten mit der Wahrscheinlichkeit 1-p. Diese Ereignis ohne die Reihenfolge zu berücksichtigen hat also die Wahrscheinlichkeit pk ‧(1-p)n-k . Wie oft kommt also dieses Ereignis vor? Man muss also k Treffer auf n Stellen kombinieren. Die Anzahl ist n über k. So erhält man also die Wahrscheinlichkeitsformel für k Treffer:
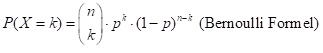
Beispiel 1: Es wird 100−mal ein „fairer“ Würfel gewürfelt. Wie groß ist die Wahrscheinlichkeit, dass 10 Sechsen gewürfelt werden?
Antwort: n = 100; p = 1/6;
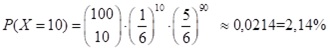
Beispiel 2: Ein Medikament verursacht mit 10% Wahrscheinlichkeit eine Nebenwirkung. In einer Praxis werden 10 Patienten behandelt. Wie groß ist die Wahrscheinlichkeit, dass
(1) höchstens ein Patient eine Nebenwirkung hat?
(2) mindestens einer eine Nebenwirkung hat?
Antwort:
(1) P(X≤1) = P(X=0) + P(X=1) ≈ 0,34868 + 0,38742 = 0,7361
(2) P(X≥1) =1−P(X=0) ≈ 1 − 0,3487 = 0,6513
Diese Untersuchungen können sehr aufwendig sein, wenn man größere Bereiche untersucht und diese Formel sehr oft anwenden und aufaddieren muss. Zur Hilfe gibt es hier Tabellen, in denen man die Summen von 0 bis k zu einer bestimmten Wahrscheinlichkeit und einer Gesamtzahl n nachschlagen kann.
Ein Beispiel einer solchen Tabelle kann für n=10 so aussehen:
| k | p = 0,1 | p = 1/6 | p = 0,2 | p=1/3 | p = 0,5 |
| 0 | 0,3487 | 0,1615 | 0,1074 | 0,0173 | 0,0010 |
| 1 | 0,7361 | 0,4845 | 0,3758 | 0,1040 | 0,0107 |
| 2 | 0,9298 | 0,7752 | 0,6778 | 0,2991 | 0,0547 |
| 3 | 0,9872 | 0,9303 | 0,8791 | 0,5593 | 0,1719 |
| 4 | 0,9984 | 0,9845 | 0,9672 | 0,7869 | 0,3770 |
| 5 | 0,9999 | 0,9976 | 0,9936 | 0,9234 | 0,6230 |
| 6 | 1,0000 | 0,9997 | 0,9991 | 0,9803 | 0,8281 |
| 7 | 1,0000 | 1,0000 | 0,9999 | 0,9966 | 0,9453 |
| 8 | 1,0000 | 1,0000 | 1,0000 | 0,9996 | 0,9893 |
| 9 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9990 |
| 10 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
Beispiel 3: a) Die Wahrscheinlichkeit für einen Gewinn an einem Spielautomaten beträgt 20%. Es wird 10−mal gespielt. Wie groß ist die Wahrscheinlichkeit, dass man
(1) genau 3−mal gewinnt?
(2) höchstens 4−mal gewinnt?
(3) mindestens 2−mal gewinnt?
(4) weniger als 2−mal gewinnt?
(5) mehr als 2−mal gewinnt?
(6) höchstens 5−mal und mindestens 2−mal gewinnt?
Antworten: Man muss also in der Tabelle in der Spalt p=0,2 nachschauen, in der aber die aufsummierten Werte stehen.
(1) P(X=3) = P(X≤3)-P(X≤2)=0,8791- 0,6778 = 0,2013
(2) P(X≤4) = ܲ0,9672
(3) P(X≥2) =1−P(X≤1) =1−0,3758 = 0,6242
(4) P(X≤1) = 0,3758
(5) P(X≥3) =1−P(X≤2) ≈ 1 − 0,6778 = 0,3222
(6) P(2≤X≤5) = P(X≤5) − P(X≤1) = 0,9936 – 0,3758 = 0,6178
5.3 Kumulierte Werte bei der Binominalverteilung (X≤ k)
Der Taschenrechner kann auch diese binominalen Wahrscheinlichkeiten und auch die kumulierten Werte (Summenwerte) ausrechnen.
Beim Casio-Taschenrechner hat man die Funktionen BinominalPD(k,n,p) für eine feste angegebene Trefferzahl k und die Funktion BinominalCD(k,n,p) für die aufsummierte Wahrscheinlichkeiten der Trefferzahlen bis k.
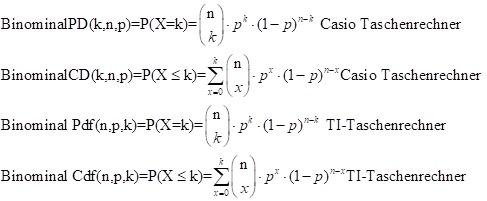
Falls der Taschenrechner diese Funktion nicht hat, so kann man auch die Formel zur Berechnung in den Taschenrechner eingeben, wobei n über k mit der nCr-Taste berechnet werden kann.
5.4 Mindestwahrscheinlichkeit und Mindestversuche
Bei der Binominalverteilung kann man aber auch noch andere Fragestellungen untersuchen.
- So kann man auch die Anzahl der Versuche berechnen, die man durchführen muss, damit man eine bestimmte Wahrscheinlichkeit von mindestens einem Treffer hat. Hier arbeitet man dann am besten mit dem Gegenereignis, da dabei weniger Fälle zu berechnen sind, also keinen Treffer zu haben.
Beispiel: Wie oft muss man Würfeln, damit man mit einer Wahrscheinlichkeit von mindestens 90% mindestens eine 6 würfelt?

- Man kann auch die Mindestwahrscheinlichkeit berechnen, damit man bei n Versuchen mit einer gewissen Wahrscheinlichkeit mindestens einen Treffer hat. Auch hier arbeitet man am besten mit dem Gegenereignis.
Beispiel: Man dreht ein Glücksrad. Wie groß muss die Gewinnwahrscheinlichkeit sein, damit man bei 10-mal drehen mit einer Wahrscheinlichkeit von mindestens 95% mindestens einmal gewinnt?

- Auch kann man die Anzahl der Versuche bestimmen, die man durchführen muss, damit man k Treffer hat mit einer gewissen Wahrscheinlichkeit. Diese Aufgabe ist meist nur mit Hilfe des Taschenrechners oder der Tabellen zu lösen, indem man versucht, sich dem Wert anzunähern.
Beispiel: Wie oft muss man Würfeln, damit man mit einer Wahrscheinlichkeit von mindestens 90% mindestens 10 mal eine 6 würfelt?

5.5 Erwartungswert, Varianz und Standardabweichung
Welche Anzahl von Erfolgen wird bei Bernoulli-Versuchen erwartet? Da man den Versuch n mal ausführt und der Erfolg mit einer Wahrscheinlichkeit p eintritt, ist der Erwartungswert n mal p und wird häufig auch mit dem griechischen Buchstaben μ bezeichnet:
μ = E(X) = n ‧ p
Führt man die Bernoulli Versuche mehrmals durch, so liegt die Anzahl der Erfolge oft in der Nähe des Erwartungswertes. Die Anzahl der Erfolge ist nicht immer der Erwartungswert, sondern es ist um den Erwartungswert gestreut. Wie weit dieser Wert um den Erwartungswert streut, berechnet man mit der Varianz bzw. der Standardabweichung. Die Varianz ist auch ein Produkt von n, p und dem Gegenereignis (1− p). V(X) = n ‧ p ‧ (1 − p)
Die Standardabweichung ist die Wurzel aus der Varianz und wird mit σ bezeichnet.
σ = √ n ‧ p ‧ (1 − p), d.h. die Varianz ist das Quadrat der Standardabweichung.
σ2 = V(X)
5.6 σ-Regel und σ-Umgebungen
Mit Hilfe der Standardabweichung kann man Intervalle um den Erwartungswert berechnen, innerhalb dessen dann die Anzahl der Erfolge liegen mit einer bestimmten Wahrscheinlichkeit. Dieses besagt die sogenannte σ-Regel, die man aber nur anwenden darf, wenn σ ≥ 3 ist.
σ- Regel: Ist σ ≥ 3 dann gilt:Die Anzahl der Erfolge eines Bernoulli Versuches liegen mit einer Wahrscheinlichkeit von 68% in der σ –Umgebung um den Erwartungswert.
Die Anzahl der Erfolge eines Bernoulli Versuches liegen mit einer Wahrscheinlichkeit von 95,5% in der 2σ –Umgebung um den Erwartungswert.
Die Anzahl der Erfolge eines Bernoulli Versuches liegen mit einer Wahrscheinlichkeit von 99,7% in der 3σ –Umgebung um den Erwartungswert.
In einer Formel ausgedrückt bedeutet dies:
P(μ – σ ≤X≤ μ + σ) ≈ 68%% (σ-Umgebung)
P(μ − 2σ ≤X≤ μ + 2σ) ≈ 95,5%% (2σ-Umgebung)
P(μ − 3σ ≤X≤ μ + 3σ) ≈ 99,7%% (3σ-Umgebung)
Beispiel: Bei einem Blumensamen ist zu erwarten, dass von 100 Samenkörnern 80 aufgehen werden. Wie groß ist die Standardabweichung und wie groß ist die Wahrscheinlichkeit, dass mindestens 72 und höchstens 88 der Samenkörner aufgehen werden?
Es gilt: μ = n∙p = 100 ‧ 0,8 = 80
Damit ergibt sich die Standardabweichung: σ = √n∙p∙ (1−p) = √100 ∙ 0,8 ∙ 0,2 = √16 = 4
Den Bereich von 72 bis 88 erhält man, indem man vom Erwartungswert 8 abzieht bzw auf den Erwartungswert 8 addiert. Der Wert 8 ist das Doppelte der Standartabweichung. Dies ist also die 2 σ-Umgebung. Nach der σ-Regel, die man hier anwenden darf, da σ≥3 ist, ist die Wahrscheinlichkeit mindestens 95,5%.
Die gesuchte Wahrscheinlichkeit kann man aber auch mit der kumulierten Wahrscheinlichkeit berechnen:
P(72 ≤ X ≤ 88) = P(X ≤ 88) − P(X < 72) = P(X ≤ 88) − P(X ≤ 71) ≈ 0,9874 − 0,0200 = 0,9674
Die Wahrscheinlichkeit, dass mindestens 72 und höchstens 88 Blumensamen aufgehen, beträgt als sogar 96,74%
Die Wahrscheinlichkeitswerte erhält man wieder im Taschenrechner mit BinominalCD oder aus der Tabelle n=100,p=0,8:
BinominalCD(88,100,0,8)=0,9874
BinominalCD(71,100,0,8)=0,0200
5.7 Aufgaben zur Binominalverteilung
Aufgabe 1: Beim Würfeln mit zwei Würfeln wird folgendes Spiel vereinbart. Bei Pasch (zwei gleich Augenzahlen) erhält man 5 €, ansonsten muss man 1 € bezahlen.
- Berechne die Wahrscheinlichkeitsverteilung und den Erwartungswert.
- Wie muss den Einsatz wählen, damit dieses Spiel fair ist?
Aufgabe 2: Berechne folgende Wahrscheinlichkeiten mit Hilfe der Tabellen.
- P(X = 40) ; n=50 ; p= 0,9
- P(X ³ 41); n = 50; p = 0,7
- P(X > 30); n = 100; p = 0,2
- P(70 £ X £ 78); n = 100; p = 0,8
- P(60 £ X £ 76); n = 400; p = 0,17
- P(150 £ X £ 165); n = 250; p = 0,62
Aufgabe 3: 42,5% aller Deutschen haben Blutgruppe A. 38% haben Blutgruppe 0. Nacheinander kommen Personen zufällig zur Blutspende beim Deutschen Roten Kreuz.
- Mit welcher Wahrscheinlichkeit hat
(1) der erste Spender, (2) erst der dritte Spender, (3) erst der fünfte Spender Blutgruppe A? - Wie viele Spender müssen kommen, damit die Wahrscheinlichkeit für mindestens einen Spender mit Blutgruppe A größer als 90% ist?
- In einer Zufallsstichprobe wird bei 100 Personen die Blutgruppe bestimmt. Gib eine Umgebung um den Erwartungswert an, in der mit einer Wahrscheinlichkeit von 90% die Anzahl der Personen mit Blutgruppe 0 liegen.
- Wie groß ist die Wahrscheinlichkeit, dass bei dieser Stichprobe die Anzahl der Personen mit Blutgruppe A zwischen 35 und 50 liegen bzw. zwischen 38 und 48 liegen?
Aufgabe 4: Eine Gärtnerei vertreibt Blumenzwiebeln, Blumensamen und Saatgut für Erbsen.
- Für die Blumenzwiebeln wird eine Keimgarantie von 90% gegeben. Jemand kauft eine Packung mit 10 Zwiebeln. Mit welcher Wahrscheinlichkeit keimen
(1) alle Zwiebeln
(2) genau 90% der gekauften Zwiebeln
(3) mehr als 90% der gekauften Zwiebeln? - Saatgut für Erbsen gibt es in 2 Güteklassen. Die 1. Wahl hat eine Keimgarantie von 90%, die 2. Wahl hat nur 75% Keimgarantie. Von einem großen Saatgutvorrat weiß man nicht, welche Güteklasse es ist. Dies soll mit 100 Stichproben getestet werden. Stelle eine Entscheidungsregel für beide Hypothese auf, so dass der Fehler 1. Art kleiner als 5% beträgt. Berechne auch den Fehler 2. Art.
- Blumensamen kann leicht durch Unkrautsamen verunreinigt werden. 100 Unkrautsamen gelangen in 100 Samentüten. Mit welcher Wahrscheinlichkeit sind in einer zufällig herausgegriffenen Tüte 0, 1, 2 und mehr als 2 Unkrautsamen? Wie viele Packungen enthalten demnach 0, 1, 2 und mehr als 2 Unkrautsamen?
- In die Abfüllmenge von 100 Samentüten sind n Unkrautsamen gelangt. Mit welcher Wahrscheinlichkeit sind in einer zufällig herausgegriffenen Tüte kein Unkrautsamen? Wie viele Packungen werden keine Unkrautsamen enthalten?
- Von 100 Sattguttüten enthielten 50 keine Unkrautsamen. Schätze aufgrund von Teilaufgabe d) die Anzahl der Unkrautsamen.
Lösungen:
Aufgabe 1:
a)
| Pasch | kein Pasch | |
| P(X) | 1/6 | 5/6 |
| X | 5 € | -1 € |
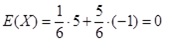
b)
| Pasch | kein Pasch | |
| P(X) | 1/6 | 5/6 |
| X | 5 € – a € | – a € |
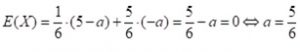

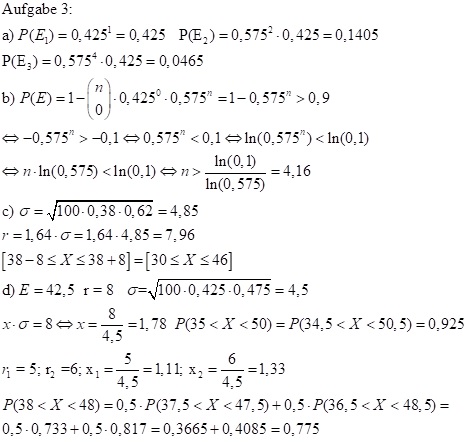

Aufgabe 5: 42,5% aller Deutschen haben Blutgruppe A. 38% haben Blutgruppe 0. Nacheinander kommen Personen zufällig zur Blutspende beim Deutschen Roten Kreuz.
a) Mit welcher Wahrscheinlichkeit hat
(1) der erste Spender
(2) erst der dritte Spender
(3) erst der fünfte Spender Blutgruppe A?
b) Wie viele Spender müssen kommen, damit die Wahrscheinlichkeit für mindestens einen Spender mit Blutgruppe A größer als 90% ist?
c) In einer Zufallsstichprobe wird bei 100 Personen die Blutgruppe bestimmt. Gib eine Umgebung um den Erwartungswert an, in der mit einer Wahrscheinlichkeit von 90% die Anzahl der Personen mit Blutgruppe 0 liegen.
d) Wie groß ist die Wahrscheinlichkeit, dass bei dieser Stichprobe die Anzahl der Personen mit Blutgruppe A zwischen 35 und 50 liegen bzw. zwischen 38 und 48 liegen?

Aufgabe 6: Eine Gärtnerei vertreibt Blumenzwiebeln und Blumensamen.

- Für die Blumenzwiebeln wird eine Keimgarantie von 90% gegeben. Jemand kauft eine Packung mit 10 Zwiebeln. Mit welcher Wahrscheinlichkeit keimen
(1) alle Zwiebeln
(2) genau 90% der gekauften Zwiebeln
(3) mehr als 90% der gekauften Zwiebeln? - Unter einer großen Lieferung Tulpenzwiebeln sind etwa ein Drittel gelb blühende Tulpenzwiebeln. Berechne den Erwartungswert und die Standardabweichung für gelb blühende Tulpenzwiebeln bei insgesamt 200 Tulpenzwiebeln. Mit welcher Anzahl von gelben Tulpen ist mit 99% Sicherheit zu erwarten? Mit welcher Wahrscheinlichkeit liegt die Anzahl gelber Tulpenzwiebeln zwischen 50 und 80 Stück?
- In die Abfüllmenge von 100 Samentüten sind n Unkrautsamen gelangt. Mit welcher Wahrscheinlichkeit ist in einer zufällig herausgegriffenen Tüte kein Unkrautsamen? Wie viele Packungen werden keine Unkrautsamen enthalten?
- Von 100 Sattguttüten enthielten 50 keine Unkrautsamen. Schätze aufgrund von Teilaufgabe c) die Anzahl der Unkrautsamen.

Aufgabe 7: Lotto 6 aus 49

- Die höchste Gewinnklasse erzielt man bei 6 Richtigen mit Superzahl (Endziffer auf dem Lottoschein (von 0 bis 9). Berechne die Wahrscheinlichkeit, diesen Höchstgewinn zu erzielen.
- Berechne die Wahrscheinlichkeit, 4 Richtige mit und ohne Superzahl zu tippen.
- Die Wahrscheinlichkeit für die Ziehung einer bestimmten Zahl bei einer Wochenziehung beträgt 6 zu 49. Mit welcher Wahrscheinlichkeit wird die Zahl 15 in 490 Wochenziehungen mindestens 54 und höchstens 66-mal gezogen?
- Bestimme die Anzahl der Wochenziehungen, mit der man mit 95% Sicherheit mindestens rechnen muss, damit die Zahl 15 mindestens einmal gezogen wird?
