2. Kombinatorik
2.1 Grundlegende Rechenformeln
Bei der Wahrscheinlichkeitsrechnung muss man sehr oft die Anzahl der Möglichkeiten berechnen. Deshalb kann man bei der Kombinatorik verschiedene Formeln aufstellen, mit denen man die Möglichkeiten und damit dann auch die Wahrscheinlichkeiten berechnen kann. Hierbei ist es aber auch wichtig zu wissen, ob dabei die Reihenfolge der wichtig oder egal ist und ob man bei den möglichen Ziehungen das gezogene wieder zurücklegt oder nicht.
Hat man n verschiedene Objekte und möchte diese in ihrer Reihenfolge anordnen, so berechnet man die Anzahl der Permutationen von n Objekten. Für das 1. Objekt hat man noch n- Möglichkeiten. Ist dieses festgelegt, so hat man für das 2. Objekt nur noch n-1 Möglichkeiten usw.
Die Anzahl der Möglichkeiten n verschiedene Objekte in ihrer Reihenfolge zu vertauschen ist demnach 1 ∙ 2 ∙ 3 ∙ … ∙n. Zu dieser Formel dem Produkt von 1 bis n sagt man auch n Fakultät und schreibt n!
Also ist n! = 1 ‧ 2 ‧ 3 ‧ … ‧(n-1) ‧n . Diese Formel „n-Fakultät“ ist auch auf vielen Taschenrechnern zu finden. Dabei ist 0! = 1.
Beispiel: Es sind 5 Pferde bei einem Rennen gestartet. Wie viele Möglichkeiten gibt es für den Zieldurchlauf? Antwort: 5! = 120 Somit gäbe es auch 120 Möglichkeiten für 5 Personen sich in einer Reihe anzustellen.
Hat man bei diesen Berechnungen der Anordnungsmöglichkeiten auch Gruppen gleicher Objekte, so hat man noch eine andere Formel zur Berechnung der Möglichkeiten.
Beispiel: Hat man die Buchstaben AAA BBBB CC so hat man zwar 9 Buchstaben aber nur drei unterschiedliche Buchstaben. Die Anzahl aller möglichen Kombinationen dieser 9 Buchstaben ist
9!/(3!‧4!‧2!) = 2‧3‧4‧5‧6‧7‧8‧9/2‧3‧2‧3‧4‧2=2‧3‧5‧6‧7 = 1260
Hat man bei einer Anzahl von n Objekten nur zwei Sorten k und (n-k), so erhält man die Anzahl von Kombinationen mit der Formel n!/k!‧(n-k)! Diese Formel wird als Binomialkoeffizient n über k bezeichnet.
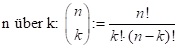
Im Taschenrechner mit der Funktion nCr zu berechnen.
Beispiel: Lotto 6 aus 49 hat bei der Ziehung 6 Richtige und 43 Falsche Kugeln. Die Anzahl der Kombinationsmöglichkeiten ist:
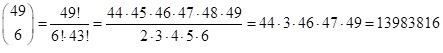
Für den Binomialkoeffizienten gilt:
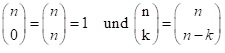
Bei diesen Beispielen wurden alle n Elemente angeordnet oder gezogen. Dieses muss aber nicht immer so sein. Man kann auch nur eine begrenzte Menge k daraus ziehen. Dann ergibt sich folgende Formel:
2.2 Ziehen ohne Zurücklegen und mit Beachtung der Reihenfolge
Aus n Elementen werden k gezogen. Dies ergibt die Formel:
n‧(n-1)‧(n-2)‧…‧(n-k+1)=n!/(n-k)! – Im Taschenrechner mit der Funktion nPr zu berechnen.
Beispiel: Wie viele Möglichkeiten gibt es theoretisch für die ersten 3 Pferde bei einem Pferderennen (mit 10 Pferden am Start), wenn man die Reihenfolge der ersten 3 Pferde betrachtet?
Antwort:
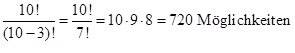
Im Taschenrechner erhält man mit 10 nPr 3 auch den Wert 720.
Ein weiteres Beispiel: Ein Verein mit 20 Mitgliedern wählt einen 1. und 2. Vorsitzenden. Wie viele Möglichkeiten gibt es theoretisch?
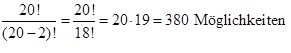
2.3 Ziehen ohne Zurücklegen und ohne Beachtung der Reihenfolge
Wenn es sich nun um n verschiedene Objekte handelt, von denen man k (ohne Beachtung der Reihenfolge) auswählen möchte, dann gibt es n über k Möglichkeiten.
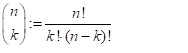
Im Taschenrechner gibt es eine Funktion, die n über k sofort berechnet. Dies ist die Taste nCr. Dazu gibt man zuerst n ein, dann die nCr Taste und dann k eingeben.
Beispiele:
(a) Ein Verein mit 20 Mitgliedern wählt einen Vorstand aus 5 Personen. Wie viele Möglichkeiten gibt es theoretisch?
20 über 5 = 16‧17‧18‧19‧20/2‧3‧4‧5=16‧17‧3‧19 = 15504
(b) In einer Klasse bestehend aus 15 Mädchen und 10 Jungs sollen 5 Mädchen und 5 Jungen ausgewählt werden. Wie viele Möglichkeiten gibt es theoretisch?
Beide Gruppen muss man einzeln betrachten und die Möglichkeiten multiplizieren. Dies ergibt:
(15 über 5) mal (10 über 5) = 11‧12‧13‧14‧15/2‧3‧4‧5 ‧ 6‧7‧8‧9‧10/2‧3‧4‧5 =
11‧3‧13‧7 ‧ 2‧7‧2‧9= 756756 Möglichkeiten
(c) Man erhält 5 Karten von 32. Wie groß ist die Wahrscheinlichkeit, dass 2 Asse, 2 Buben und 1 Dame mit dabei sind (falls es 4 Asse, 4 Buben und 4 Damen gibt)?
Antwort: Die Gesamtzahl aller Möglichkeiten bei 5 aus 32 Karten sind 32 über 5. Günstig für den betrachteten Fall sind (4 über 2) mal (4 über 2) mal (4 über 1) mal (20 über 0). Dies ergibt die Wahrscheinlichkeit:
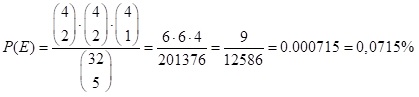
2.4 Ziehen mit Zurücklegen und mit Betrachtung der Reihenfolge
Werden aus n verschiedenen Objekten k mit Zurücklegen und mit Beachtung der Reihenfolge ausgewählt, so gibt es nk Möglichkeiten.
Beispiele:
(a) Bei einem Spielautomaten gibt es 4 Felder mit jeweils 5 verschiedenen Symbolen. Wie viele Möglichkeiten gibt es (die im Display angezeigt werden können)?
Antwort: 54 Möglichkeiten.
(b) Ein Autokennzeichen besteht aus 2 Buchstaben und 3 Ziffern. Wie viele Möglichkeiten gibt es, falls theoretisch jede Kombination an Buchstaben zugelassen wäre?
Antwort: 262 ∙ 9 ∙ 102 = 608.400, da die erste Ziffer keine Null sein darf.
2.5 Ziehen mit Zurücklegen und ohne Betrachtung der Reihenfolge
Werden aus n verschiedenen Elementen k mit Zurücklegen und ohne Beachtung der Reihenfolge gezogen, so gibt es (n + k – 1) über k Möglichkeiten. Dabei sind n die unterschiedlichen Töpfe, k sind die Ziehungen. Hierbei sollen eine Anzahl nicht unterscheidbarerer Objekte k auf mehrere Bereiche n verteilt werden z.B. 12 Personen auf 5 Zimmer oder 15 Bälle in 4 Ballnetze usw.
Beispiel1: Es sollen 10 Kugeln auf 4 Schachteln verteilt werden. Dies wäre auch das mathematische Modell, wenn man 10 Personen auf 4 Zimmer verteilen möchte. Um die Rechnung zu verdeutlichen kann man die 10 Kugeln als x und die Trennung der Schachteln als | bezeichnen, wobei man dafür statt 4 drei zur Abtrennung braucht (k-1). xxxxxxxxxx||| muss man jetzt in der Reihenfolge tauschen.
xx|xxx|x|xxxx wäre eine mögliche Verteilung. In Schachtel 1 sind 2 in Schachtel 2 sind 3 in Schachtel 3 sind 1 und in Schachtel 4 sind 4 Kugeln. Die Anzahl der Möglichkeiten der x-en ist dann 13 über 10. Dies ergibt dann 286 Möglichkeiten.
Beispiel2: 12 Personen auf 5 Zimmer verteilen: n = 5; k = 12
16 über 12 =1820 Möglichkeiten
Beispiel3: 15 Bälle in 4 Ballnetze verteilen: n=4; k = 15
18 über 15 = 816 Möglichkeiten.