2. Geradengleichung
Geraden gehören zu den grundlegenden Objekten der analytischen Geometrie. Es handelt sich dabei um eine „gerade“ Linie, die sich ohne Anfangs- und Endpunkt bis ins Unendliche erstrecken. Auf einer Geraden liegen unendlich viele Punkte.
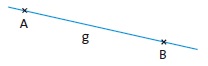
Eine Gerade g wird entweder durch zwei Punkte A und B eindeutig festgelegt oder durch einen Punkt A und eine Richtung der Geraden. Den Vektor zum Punkt A nennt man Ortsvektor a→ und den Vektor für die Richtung der Geraden nennt man Richtungsvektor c→, der angibt, in welche Richtung die Gerade verläuft. Hierfür kann man den Vektor zwischen A und B nehmen. Es ist aber jeder andere Vektor auch möglich, der auf der Geraden liegt, also zwei Punkte der Geraden miteinander verbindet.
2.1. Die Parameterdarstellung von Geraden
Man gelangt nun zu jedem beliebigen Punkt der Geraden, in dem man zunächst mit dem Ortsvektor a→ auf die Gerade gelangt und daran den Richtungsvektor anlegt, den man aber noch beliebig lang machen kann und auch in die andere Richtung drehen kann. Dies erreicht man durch eine skalare Multiplikation des Richtungsvektors (Vervielfachung oder Verkürzung).
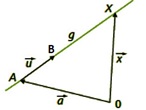

Setzt man nun für r Zahlen ein, so erreicht man jeden beliebigen Punkt x der Geraden g. Für r=1erhält man den Punkt B(-1|1|2), mit r=2 erreicht man den Punkt C(-6|4|1). Man kann unendlich viele Zahlen für r einsetzen und erhält unendlich viele Punkte der Geraden.
2.2. Die Punktprobe
Durch Einsetzen des Ortsvektors zum Punkt P für den beliebigen Vektor x→ kann man prüfen, ob der Punkt P auf der Geraden g liegt. Diese Rechnung nennt man Punktprobe. Liegt der Punkt P(12|-16|4) auf der Geraden g?

Aufgabe 1: Die Punkte A(-1|3|4) und B(2|-2|1) liegen auf einer Geraden.
- Berechne den Abstand zwischen den Punkten A und B.
- Bestimme eine Geradengleichung der Geraden g in Parameterform, auf der beide Punkte A und B liegen.
- Gebe mindestens noch 5 weitere Punkte der Geraden an.
- Liegen die Punkte C(-4|2|-2), D(6|3|-6) oder E(-7|13|10) auf der Geraden g?
Aufgabe 2: Gegeben sind die drei Punkte A(2|-3|2), B(-3|2|-1) und C(-1|0|4).
- Berechne eine Parameterdarstellung der Geraden g, auf der die Punkte A und B liegen.
- Überprüfe, dass die drei Punkte A, B und C ein Dreieck bilden.
- Berechne den Umfang des Dreiecks.
- Bestimme die Größe der Innenwinkel und prüfe die Winkelsumme im Dreieck.
Aufgabe 3: Ein Flugzeug fliegt in einer Minute auf einer Flugroute von
P(-3|2|9) nach Q(1|-1|9), wobei die dritte Koordinate die Flughöhe darstellt und die Koordinaten in km angegeben sind.
- Bestimme eine Geradengleichung für die Flugroute.
- Wie schnell fliegt das Flugzeug in km/h?
- Wo befindet sich das Flugzeug nach 45 Minuten?
- Nach einer Stunde setzt das Flugzeug zum Sinkflug an, wobei der Richtungsvektor sich halbiert und in der 3. Koordinate die Höhe um 1 abnimmt. An welcher Stelle befindet sich das Flugzeug dann in 1000 m Höhe?
2.3. Lagebeziehungen von Geraden
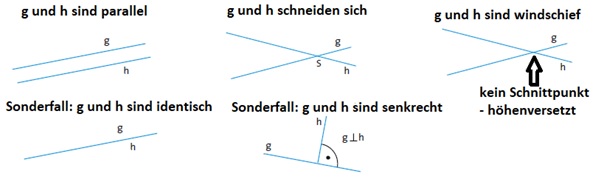
Betrachtet man nun zwei Geraden im 3-dimensionalen Raum, so können sie unterschiedlich zueinander verlaufen. Diese verschiedenen Fälle kann man sich an folgenden Skizzen verdeutlichen:
Beispiel:
Parallele Geraden haben keinen Punkt gemeinsam oder sie sind identisch. Senkrechte Geraden schneiden sich unter einem rechten Winkel.
Wenn sich zwei Geraden in der Ebene (im Zweidimensionalen) schneiden, haben sie genau einen Punkt gemeinsam. Im (dreidimensionalen) Raum können Geraden auch windschief zueinander stehen, also weder parallel sein noch einen Schnittpunkt haben.

Untersuchung der Lagebeziehung:
- Man prüft zunächst auf Parallelität. Dazu untersucht man, ob die Geraden in die gleiche Richtung verlaufen, d.h. die Richtungsvektoren in die gleiche oder entgegengesetzte Richtung zeigen. Dieses prüft man, in dem man nachweist, dass die Richtungsvektoren Vielfache voneinander sind. Es reicht aber dabei zu zeigen, dass ein Richtungsvektor ein Vielfaches des anderen Richtungsvektors

- Nun können g und h aber auch noch identisch Hierbei reicht es zu zeigen, dass g und h einen Punkt gemeinsam haben. Dann haben sie auch alle Punkte gemeinsam, da die Geraden ja in die gleiche Richtung verlaufen. Am leichtesten prüft man einen Ortsvektor, ob dieser ein Punkt der anderen Geraden ist.

- Die Geraden hätten sich auch schneiden können, wenn bei der Parallelität ein Widerspruch als Ergebnis heraus gekommen wäre. Dann muss man die Geraden auf einen gemeinsamen Punkt untersuchen. Dazu setzt man die Geradengleichungen gleich und löst das Gleichungssystem. Beachte hier aber, dass man für die beiden Parameter auch eine unterschiedlich Variable benutzt. Diese müssen ja nicht gleich sein. Mit einer eindeutigen Lösung kann man dann auch den Schnittpunkt bestimmen, in dem man einen der Parameter in die entsprechende Geradengleichung einsetzt.

Falls man bei der Schnittpunktberechnung keine eindeutige Lösung heraus bekommt, so schneiden sich die Geraden nicht. Wenn sie dann auch nicht parallel sind, so sind diese beiden Geraden windschief. Sie verlaufen aneinander vorbei. Dies geht aber nur im 3-dimensionalen Raum. Im 2-Dimensionalen geht dies nicht.
2.4. Schnittwinkel bei schneidenden Geraden
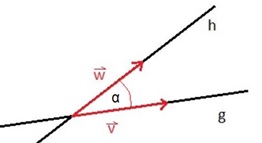
Wie im Beispiel oben berechnet schneiden sich die Geraden g und h in einem Punkt S. Hier bilden die Geraden auch einen Schnittwinkel. Je nachdem welchen Winkel man betrachtet oder berechnet, kann dieser spitz oder stumpf sein. Ausschlaggebend für den Schnittwinkel sind die beiden Richtungsvektoren, von denen man mit der Kosinus-Formel einen Winkel zwischen diesen beiden Vektoren berechnen kann. Damit man immer den spitzen Winkel berechnet, so muss man bei der Berechnung den Kosinuswert positiv machen. Dies geschieht dadurch, dass man in der Formel im Zähler, wo das Skalarprodukt steht, Betragsstriche setzt.

2.5. Abstände bei Geraden
Man kann verschiedene Abstände berechnen. Hier kann man den Abstand eines Punktes zu einer Geraden bestimmen oder auch den Abstand zweier Geraden, wenn sie sich nicht schneiden.
(1) Abstand Punkt P zur Geraden g
Da der Abstand immer als kürzester Abstand zu verstehen ist, muss man die senkrechte Verbindungslinie zwischen Gerade und Punkt finden. Der gesuchte Punkt auf der Geraden, dessen Verbindungslinie zum Punkt P senkrecht auf g steht, nennt man Lotfußpunkt F. Man fällt also das Lot von P auf die Geraden g. Dieses Verfahren nennt man auch Lotfußpunktverfahren.


(2) Abstand paralleler Geraden
Da der Abstand bei parallelen Geraden überall gleich ist, reicht es hier, einen beliebigen Punkt der Geraden zu nehmen und den Abstand zu der anderen Geraden auch wieder mit dem Lotfußpunktverfahren zu berechnen. Für den Punkt der Geraden kann man am einfachsten den Ortsvektor der Geraden nehmen.
(3) Abstand windschiefer Geraden
Auch hier muss man wieder den kürzesten Abstand zwischen diesen beiden Geraden berechnen. Dieser wird auch wieder senkrecht gemessen. Hier kennt man aber leider beide Punkte der beiden Geraden nicht, bei denen dann der Verbindungsvektor senkrecht zu beiden Geraden verläuft. Somit suchen wir hier zwei Lotfußpunkte P und Q. Der Verbindungsvektor steht sowohl auf g als auch auf h senkrecht.
