1. Vektoren und Punkte
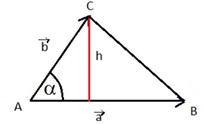
Ein Vektor ist in der Mathematik oder Physik ein Pfeil (Kraftpfeil): ein geometrisches Objekt, das eine Länge hat und außerdem in eine bestimmte Richtung zeigt.
In den meisten Fällen behandeln wir nur Vektoren mit 2 Koordinaten (x und y oder x1 und x2), was eine Vektor in einer Fläche ergibt oder mit drei Koordinaten (x, y und z oder x1, x2 und x3), was einen Vektor im 3-dimensionalen Raum darstellt.
1.1. Länge eines Vektors
Die Länge des Vektors nennt man seinen Betrag |v →|. Die Länge des Vektors kann man mit Hilfe des Satzes vom Pythagoras berechnen.
Daraus ergibt sich die Formel für die Länge
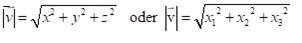
1.2. Richtungs- oder Verbindungsvektor
Neben der Länge eines Vektors ist auch noch seine Richtung ausschlaggebend. Die Lage im Raum oder der Ebene ist beliebig. Alle Vektoren mit gleicher Länge und gleicher Richtung nennt man vektorgleich.
Die Richtung eines Vektors kann man z. B. durch einen Anfangs- und einen Endpunkt angeben. Der Vektor PQ→ ist also die Verbindung zwischen den Punkten P und Q, wenn man sie von P aus in Richtung Q abgeht. Man berechnet den Vektor PQ→ , indem man die Koordinaten von Q nimmt und davon die Koordinaten von P abzieht (Zielpunkt – Anfangspunkt. Die Koordinaten der Vektoren werden in einer Klammer untereinander geschrieben. Dies ist der Unterschied zu einem Punkt, dessen Koordinaten man in einer Klammer nebeneinander schreibt.

1.3. Abstand zweier Punkte
Die Länge dieses Vektors und somit den Abstand von P zu Q berechnet man mit der Längenformel eines Vektors.
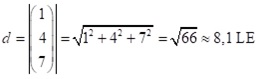
1.4. Besondere Vektoren
Besondere Vektoren sind der Gegenvektor, der in die entgegengesetzte Richtung verläuft. Hier werden die Vorzeichen in allen Koordinaten gewechselt und der Nullvektor, der in allen Koordinaten Null ist.

Ein Vektor, dessen Länge genau 1 ist, heißt Einheitsvektor der jeweiligen räumlichen Richtung. Man kann einen jeden beliebigen Vektor zu einem Einheitsvektor machen, indem man ihn durch seine Länge teilt. Man nennt diesen Vektor auch „normierter Vektor“.
1.5. Rechenregeln für Vektoren
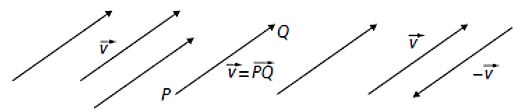
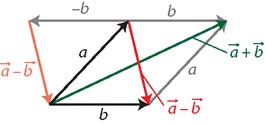
Man kann Vektoren addieren und subtrahieren. Diese kann man entweder koordinatenweise aufschreiben (siehe unten), oder sich auch grafisch darstellen (siehe Abbildung).
- Man addiert zwei Vektoren, indem man den Startpunkt des einen Vektors an die Spitze des anderen legt. Der Summenvektor verläuft dann vom Startpunkt des ersten zur Spitze des zweiten Vektors. Hier werden die beiden Vektoren aneinander gelegt.
Man subtrahiert zwei Vektoren, indem man den Gegenvektor addiert. So erhält man den Vektor, der die beiden Spitzen der Vektoren miteinander verbindet.

Wie bei normalen Zahlen gelten auch für die Vektoraddition die folgenden Rechengesetze:
- Kommutativgesetz: a→+ b→ = b→ +a→ (Vertauschungsgesetz)
- Assoziativgesetz: a→ + (b→ + c→) = (a→ +b→) + c→ (Klammerregel)-Klammern werden zuerst berechnet
- Multiplikation von Vektoren:
Bei der Multiplikation ist es dagegen etwas komplizierter als bei normalen Zahlen. Es gibt hier drei verschiedene Multiplikationen:
a) Bei der skalaren Multiplikation wird eine Zahl mit einem Vektor multipliziert. Das Ergebnis dieser Multiplikation ist dann wieder ein Vektor. Geometrisch betrachtet ergibt diese skalare Multiplikation eine Verlängerung oder Verkürzung eines Vektors. Ist der skalare Faktor negativ, so dreht sich der Vektor auch noch in die entgegen gesetzte Richtung. Mathematisch wird jede Koordinate des Vektors mit der gleichen reellen Zahl multipliziert. Der Ausdruck „Skalar“ ist dabei einfach eine in der Vektorrechnung gebräuchliche andere Bezeichnung für eine gewöhnliche Zahl.

b) Beim Skalarprodukt werden zwei Vektoren miteinander so multipliziert, dass das Ergebnis eine reelle Zahl ist. Deshalb wird es Skalarprodukt genannt. Das Skalarprodukt wird zur Untersuchung von Winkeln benötigt. Teilt man das Skalarprodukt noch durch beide Längen der Vektoren, so erhält man den Kosinus des eingeschlossenen Winkels. Beim Skalarprodukt werden die jeweiligen Koordinaten multipliziert und diese Ergebnisse addiert. Dies ergibt folgende Regel für das Skalarprodukt:
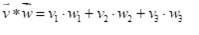
1.6. Winkel zwischen zwei Vektoren
Mit dem Skalarprodukt und den Längen der Vektoren kann man den Winkel zwischen zwei Vektoren berechnen. Der Bruch aus Skalarprodukt geteilt durch das Produkt der beiden Längen ergibt den Kosinuswert des Winkels zwischen diesen Vektoren. Dieser Winkel kann spitz also kleiner als 90o (0<cos(α)<1) aber auch stumpf also zwischen 90o und 180o sein (‒1<cos(α)<0). Für den Winkel zwischen zwei Vektoren ergibt sich folgende Formel:
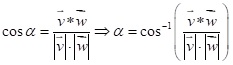
Im Zähler steht das Skalarprodukt, wobei die jeweiligen Koordinaten miteinander multipliziert und die Ergebnisse addiert werden. Im Nenner stehen die beiden Längen – also muss man das Skalarprodukt durch die beiden Längen teilen.
Ist das Skalarprodukt Null, so stehen die beiden Vektoren senkrecht zueinander,
da der cos-1(0) = 90o ist.
Beispiel: Berechne den Winkel α im Dreieck ABC mit A(1|2|-2), B(-2|3|5) und C(0|-3|2).
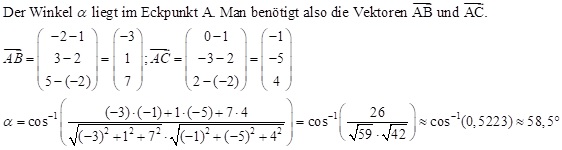
1.7. Das Kreuzprodukt für den Normalenvektor
Das Kreuzprodukt bzw. Vektorprodukt (Vektor mal Vektor, ergibt einen Vektor). Dieses Kreuzprodukt ist eine komplizierte Berechnung. Das Ergebnis ist ein Vektor, der eine besondere Eigenschaft aufweist. Dieser Vektor steht auf beiden Vektoren senkrecht und wird auch deshalb Normalenvektor genannt. In der Mathematik ist eine Normale auch eine Senkrechte.
Beim Kreuzprodukt werden jeweils zwei Koordinaten überkreuz miteinander multipliziert und voneinander subtrahiert. Dabei fängt man immer rechts oben an und multipliziert mit der darunter stehenden Koordinate links minus links oben mal der darunter stehenden Koordinate rechts. Da so jeweils ein Kreuz entsteht, nennt man dieses Produkt auch Kreuzprodukt. Zur Berechnung kann man sich ein Hilfsmittel zu Nutze machen, indem man beide Vektoren nochmals darunter schreibt und die erste und letzte Zeile oder Koordinate von den sechs Koordinaten streicht. . Man multipliziert nun angefangen in der 2. Zeile über Kreuz nach unten links in der 3. Koordinate minus über Kreuz von rechts unten (3. Koordinate) nach links oben (2. Koordinate). Dann die 3. und 4. Zeile und die 4. und 5. Zeile genauso. Dies ergibt folgende Formel für das Kreuzprodukt.
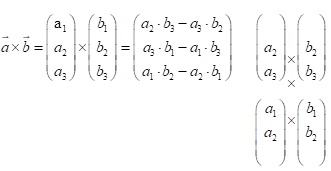
1.8. Mittelpunkt
Den Mittelpunkt einer Strecke berechnet man, in dem man die Mittelwerte der einzelnen Koordinaten berechnet.
Bei den Punkten A(a1|a2|a3) und B(b1|b2|b3) ist der Mittelpunkt M((a1+b1)/2|(a2+b2)/2|(a3+b3)/2).
Beispiel: A(-2|3|4) und B(-6|-1|2) hat den Mittelpunkt M(-4|1|3).
Man könnte zur Berechnung aber auch den Ortsvektor zum Punkt A nehmen und auf ihn die Hälfte des Richtungsvektors AB addieren. So gelangt man zum Mittelpunkt.
1.9. Flächeninhalte
(1) Parallelogramm

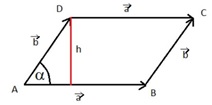
(2) Dreieck
Da der Flächeninhalt des Dreiecks nur die Hälfte des Parallelogramms ist, erhält man die Flächenformel eines Dreiecks durch Halbierung der Flächenformel des Parallelogramms.