4. Ableitungen
4.1. Der Ableitngsbegriff
Einführungsbeispiel:
Eine Rakete startet von einer Startrampe, deren Höhen nach dem Start in unterschiedlichen Abständen gemessen werden.
|
Zeit t in Sekunden |
1,30 |
2,50 |
3,50 |
4,35 |
5,00 |
6,35 |
|
Höhe h in Meter |
9,9 |
22,0 |
34,9 |
47,4 |
59,1 |
85,7 |
Wir ermittelten aus realen Messwerten einen mathematisch funktionalen Zusammenhang. Grundgedanken des physikalischen Zusammenhangs: Die Rakete beschleunigt beim Start, deshalb erscheint ein quadratischer Zusammenhang zwischen h und t sinnvoll. h(t)=1/2 a‧t2 + v0‧t + h0
mit a = Beschleunigung; v0 = Anfangsgeschwindigkeit und h0 = Anfangshöhe
Gibt man die Messwerte in einen Computer ein, so erhält man die Funktion:
h(t )= 1,305t2 + 5,017t + 1,221
Beschleunigung 2,61 m/s2, Anfangsgeschwindigkeit 5,02 m/s, Starthöhe 1,22 m
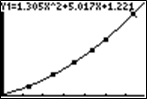
Man möchte nun die Geschwindigkeit der Rakete berechnen. Die Geschwindigkeit ist ja ein Verhältnis von Weg zu Zeit (km/h). Dieses lässt sich nun aus den Messwerten der Höhe bzw. aus der Funktionsgleichung berechnen – leider aber nur für bestimmte Zeitbereiche, also ein Mittelwert für jeden Bereich. Dieses nennt man die mittlere Änderungsrate oder die mittlere Geschwindigkeit.
Die mittlere Geschwindigkeit bzw. Änderungsrate berechnet man mit dem Quotienten aus Weg und Zeit zwischen zwei Zeitpunkten
f(b) – f(a)
Definition: b – a bezeichnet man als Differenzenquotient
oder (mittlere) Änderungsrate der Funktion f im Intervall [a; b] ,
dies ist hier die mittlere Geschwindigkeit bzw. die Sekantensteigung.
Berechne für die 3 Zeitintervalle die mittlere Geschwindigkeit bzw. die Durchschnittsgeschwindigkeit.
| Zeit t in Sekunden | 1,30 | 2,50 | 3,50 | 4,35 | 5,00 | 6,35 |
| Höhe h in Meter | 9,9 | 22,0 | 34,9 | 47,4 | 59,1 | 85,7 |
| Durchschnitts- geschwindigkeit |
12,1:1,2= 10,08 m/s |
12,5:0,85= 14,7 m/s |
26,6:1,35= 19,7m/s |
|||
Die Geschwindigkeit nimmt natürlich in den Zeitintervallen aufsteigend zu, da die Rakete ja immer schneller wird. Diese Berechnung ist aber nur eine mittlere Geschwindigkeit in diesen Intervallen. Die momentane oderexakte Geschwindigkeit bzw. Änderungsrate an einer festen Stelle kann man nur näherungsweise berechnen. Dazu muss man das Intervall beliebig klein werden. Somit lässt man die Differenz h der beiden Stellen beliebig klein werden, so spricht man von der Berechnung eines Grenzwertes h gegen Null. Dies nennt man die Momentangeschwindigkeit bzw. die momentane Änderungsrate oder die Steigung an einer Stelle. Es wird als Ableitung bezeichnet.
f(a + h) – f(a)
Definition: f ´(a) = lim h bezeichnet man als
h→0
Grenzwert des Differenzenquotienten oder auch als Ableitung an der Stelle a, hier ist es die Momentangeschwindigkeit bzw.
die Tangentensteigung oder die momentane Änderungsrate.
| Zeit t in Sekunden | 1,30 | 2,50 | 3,50 | 4,35 | 5,00 | 6,35 |
| Höhe h in Meter | 9,9 | 22,0 | 34,9 | 47,4 | 59,1 | 85,7 |
| Momentan-geschwindigkeit | 8,41m/s | 11,5m/s | 14,2m/s | 16,4m/s | 18,1m/s | 21,6m/s |
Die Ableitungsfunktion ist wie im Beispiel die Geschwindigkeits-Funktion. Die Funktionswerte sind dabei die Steigung der Ausgangsfunktion f und wird mit f´(x) (f Strich von x) bezeichnet.
f(x+h) – f(x)
Definition: f´(x) = lim h bezeichnet man als
h→0
Grenzwert des Differenzenquotienten an einer beliebigen Stelle x oder auch als Ableitungsfunktion an der Stelle x, die für jede Stelle x die momentane Geschwindigkeit bzw. die Steigung der Tangente angibt.
Beispiel:
Betrachten wir das Schaubild der Funktion
f(x) = x2 –3x + 2
Wie ändert sich der Funktionswert im Intervall [2 ; 3]?
Er ändert sich um 2, denn f(2) = 0 und f(3) = 2.
Die mittl. Änderungsrate der Funktion f im Intervall [2 ; 3] ist somit (2 – 0)/(3– 2) = 2/1 = 2.
(vgl. „Steigungsdreieck“: 1 nach rechts, 2 nach oben)
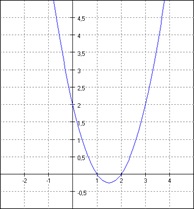
Der Differenzenquotient der Funktion f(x) im Intervall [2 ; 3] ist 2.
Die mittlere Änderungsrate der Funktion f(x) im Intervall [2 ; 3] ist 2.
Um die momentane Änderungsrate von f bei X0 zu berechnen, müssen wir den Differenzenquotienten von f im Intervall [2 ; 2+h] für den Grenzwert h gegen 0 berechnen.
Die momentane Änderungsrate der Funktion f(x) bei X0=2 ist 1.
Die Steigung der Tangente bei bei X0 = 2 ist 1.
Wir wollen nun die Ableitung von f an der Stelle X0 zu jedem beliebigen x-Wert bestimmen, d.h. wir suchen eine Funktion f´ (die sogenannte Ableitung von f ),
die zu jedem beliebigen x-Wert die zugehörige Steigung der Tangente angibt. Dieses erhält man, wenn man den Grenzwert des Differenzenquotienten allgemein für x berechnet.
Die Funktion y = f´(x) heißt Ableitung oder Ableitungsfunktion von f.
Wir bilden allgemein für ein beliebiges x die Ableitung von f an der Stelle x:
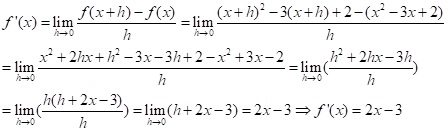
Ergebnis:
Durch Ableitung der Funktion f(x) = x2 – 3x + 2 haben wir nun schließlich deren Ableitungsfunktion f´(x) = 2x – 3 berechnet. Damit kann man die Steigung der Tangente von f an jeder beliebigen Stelle X0 sofort angeben.
Übungen:
Berechne zunächst die Steigung an der gegebenen Stelle und dann die Ableitungsfunktion.
- f(x) = 0,25x2 an der Stelle x0 = 2
- f(x) = x3 an der Stelle x0 = 1
4.2. Die Ableitungsregeln
Man muss aber nicht immer die Funktionen mit Hilfe des Grenzwertes des Differenzenquotienten (Grenzwert der Sekanten-Steigung) berechnen. Die Beispiele zeigen, dass eine gewisse Gesetzmäßigkeit bei ganz-rationalen Funktionen zu erkennen ist. Daraus kann man folgende Regeln herleiten, die im Folgenden dann auch immer benutzt werden können.
Potenzregel:
Die Ableitung der Potenzfunktionf(x)=xn ist f´(x)=n‧ xn – 1 .
Summen- und Differenzregel:
Die Ableitung einer Funktion f , die sich durch Addition bzw Subtraktion aus zwei Einzelfunktionen g und h zusammensetzt, also f = g ± h , ist f´= g´± h´.
Faktorregel:
Die Ableitung einer Funktion f , die das c-fache einer Funktion g ist, also f = c ‧ g
ist f´= c ‧ g´.
Höhere Ableitungen:
Leitet man die Ableitungsfunktion wieder ab, so erhält man die 2. Ableitung, dann die 3. Ableitung usw. Dabei wird der Grad der ganzrationalen Funktion immer kleiner.
Schreibweise: f´´(x), f´´´(x), f(4)(x), …
Eine ganzrationale Funktion vom Grad n ≥ 1 ist differenzierbar (ableitbar)
und ihre Ableitung ist eine ganzrationale Funktion vom Grad n – 1.
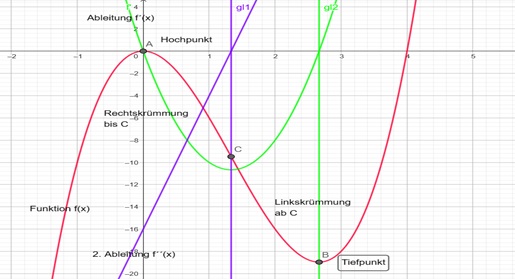
→ Der Wert der 1. Ableitung von f an einer Stelle gibt die Steigung von f an.
→ Der Wert der 2. Ableitung von f an einer Stelle gibt die Krümmung von f an.
Rechtskrümmung
Linkskrümmung
Man kann sich dies leicht veranschaulichen:
bedeutet: Die Steigung von ist negativ ( nimmt also monoton ab).
D.h.: die Steigung von f nimmt ab. (anschaulich: Rechtskrümmung des Schaubildes von ).
4.3. Beispiele von Ableitungsfunktionen
Mit Hilfe der Potenzregel lassen sich nicht nur alle Polynome von x ableiten, sondern auch Funktionen, wo eine Potenz von x im Nenner steht oder es sich um eine Wurzel von x handelt. Dies funktioniert, da man eine Wurzel oder eine Potenz von x im Nenner als Potenz von x schreiben kann. Beispiel:
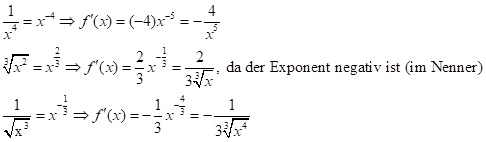
Hier sind einige wichtige Beispiele von Ableitungsfunktionen.
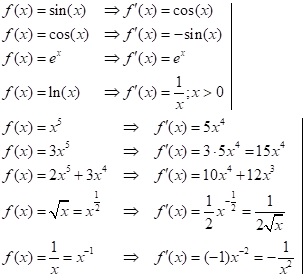
4.4. Aufgaben
Aufgabe 1: Berechne die Steigung der Funktion f an der Stelle x0 mit dem Grenzwert des Differenzenquotienten.
- f(x) = 2x2 + 2 x0 = 3
- f(x) = 4x2 – 3x x0 = –2
- f(x) = 5x3 x0 = 4
Aufgabe 2: Berechne die Ableitungsfunktion von f(x) mit dem Grenzwert des Differenzenquotienten.
- f(x) = 3x2 – 5
- f(x) = 5x2 + 4x
- f(x) = 6x3
Aufgabe 3: Berechne die Ableitungsfunktion von f(x) mit den Ableitungsregeln. Bestimme damit dann die Gleichung der Tangenten an der Stelle x = 3.
- f(x) = 7x2 – 4x
- f(x) = – 3x2 + 7x
- f(x) = – 8x3 + 5x2 – 6x
Aufgabe 4: Gegeben ist die Funktion f mit f(x) = x4 – 6x2 +5
- Berechne die Nullstellen von f(x).
- Bestimme die Stellen von f(x), an denen die Funktion die Steigung Null hat.
- Skizziere f(x) und darunter die Ableitungsfunktion. In welchen Bereichen ist f(x) monoton steigend bzw. fallend.
Aufgabe 5: Die Bewegung eines Fahrzeuges wird in den ersten Sekunden näherungsweise durch das Zeit-Weg-Gesetz s(t) = 0,25t3 – 3,5t2 + 12,25t (Weg in Meter) beschrieben.
- Welchen Abstand hat das Fahrzeug nach 2s vom Startpunkt?
- Wie groß ist die mittlere Geschwindigkeit zwischen 1 s und 3s?
- Wie groß ist die Momentan Geschwindigkeit nach genau 2s?
- Wann hat das Fahrzeug die Geschwindigkeit Null?
Aufgabe 6: Gegeben ist die Funktion f(x)= 2x2+1
- Berechne die Steigungen der Funktion f(x) beliebig und speziell an der Stelle a=-3.
- An welcher Stelle hat die Funktion die Steigung m = 2?
- Wo hat die Funktion die gleiche Steigung wie g(x)=3x+5?
- Gibt es Punkte auf dem Funktionsgraphen, an denen der Steigungswinkel 45o ist?
Aufgabe 7: Gegeben ist die Funktion f(x) = 3x2.
- Bestimme mit Hilfe der h-Methode die Ableitungsfunktion der Funktion f(x).
- Berechne mit Hilfe der h-Methode die Steigung der Funktion f(x) an der Stelle x1=1.
- An welcher Stelle hat f(x) die Steigung m = 7?
- Bestimme die Tangentengleichung an den Graphen von f(x) im Punkt P(2 | y ).
Aufgabe 8: Gegeben ist die Funktion f(x) = 3x2 +12.
- Berechne eine Tangente an die Funktion an der Stelle x=2.
- Bestimme eine Tangente an die Funktion mit der Steigung m = 4.
Wo schneidet diese Gerade die Koordinatenachsen?