3. Quadratische Funktionen
3.1. Allgemeines
Eine Funktion, deren Funktionsgleichung man als
y= ax2+bx+c schreiben kann, heißt quadratische Funktion, deren Verlauf eine Parabel darstellt. D=ℝ
z.B. y = 2x2+3x-2
Die Funktion y = x2 nennt man Normalparabel. Ihr tiefster Punkt liegt im Koordinatenursprung. Diesen Punkt nennt man Scheitelpunkt.

3.2. Nullstellen
Möchte man die Nullstellen (Schnittpunkte mit der X-Achse) einer quadratischen Funktion berechnen, so setzt man den Funktionsterm gleich Null (y = 0 oder f(x) = 0). Falls man vor dem x2 noch einen Faktor hat, der von 1 verschieden ist, so muss man die ganze Gleichung noch durch diesen Faktor teilen. So erhält man die Normalform einer quadratischen Gleichung x2+px+q = 0.
Für diese Normalform gibt es eine Lösungsformel, die sogenannte. p q-Formel.
x2+px+q = 0 hat folgende Lösungen:
x1/2 = –p/2 ±√((p/2)2 – q); (p/2)2 – q = D (Diskriminante)
D > 0 → zwei Lösungen
D = 0 → eine Lösung
D < 0 → keine Lösung
Beispiel: Berechne die Nullstellen der Parabel y = 2x2+4x–10.
Lösung: 2x2 + 4x –16 = 0 |:2↔x2 +2x –8 = 0
Lösungsformel: p = 2; q = –8
x1/2 = –2/2 ±√((2/2)2 – (-8))= –1 ±√(1+8) = –1 ± 3
x1 = 2; x2 = –4
Die Nullstellen liegen bei N1(2|0) und N2(–4|0)
3.3. Scheitelpunktform
Die Normalparabel f(x)=x2 hat den Scheitelpunkt bei S(0|0). Diese Normalparabel kann man folgendermaßen verändern:
Durch Addition bzw. Subtraktion verschiebt sich der Scheitelpunkt nach oben oder unten.
Durch Multiplikation vor dem Quadrat wird die Parabel steiler (gestreckt) oder flacher (gestaucht).
Ist dieser Faktor negativ, so ist die Parabel nach unten geöffnet.
Durch Addition bzw. Subtraktion verschiebt sich der Scheitelpunkt nach links bzw. rechts.
Somit ergibt sich folgender Satz:
Hat eine quadratische Funktion die Form y = a(x – f)2 + e,
so nennt man diese Darstellung die Scheitelpunktform einer quadratischen Funktion. An ihr kann man die Lage des Scheitelpunktes ablesen, d.h. der Scheitelpunkt liegt bei S(e | f).
Für den Faktor a gilt:
a > 0 → Die Parabel ist nach oben geöffnet.
a < 0 → Die Parabel ist nach unten geöffnet.
-1 < a <1 → Die Parabel ist gestaucht (flacher).
a < –1 oder a > 1 → Die Parabel ist gesteckt.
Damit man die Lage des Scheitelpunktes ablesen kann, muss man die quadratische Funktion in die Scheitelpunktform überführen, indem man den Teil mit x quadratisch ergänzt, so dass man die 1. oder 2. binomische Formel anwenden kann.
Beispiel: Gegeben ist die Parabel f(x) = 2x2 – 16x + 6 | Faktor 2 bei x2 und x ausklammern
= 2(x2 – 8x) + 6 |Klammer quadratisch ergänzen – halbieren und quadrieren
=2(x2 – 8x +16 – 16) +6 |binomische Formel
=2((x – 4)2– 16) + 6 |ausmultiplizieren
=2(x – 4)2 – 32 +6 |zusammen fassen
=2(x – 4)2 – 26 |Scheitelpunkt ablesen
→S(+4|-26)
Hat man den Scheitelpunkt und den Streckungsfaktor gegeben, so erhält man aus der Scheitelpunktform folgendermaßen die Normalform einer quadratischen Funktion:
Beispiel: a = 2 und S(3|5)
f(x) = 2(x – 3)2 +5 |binomische Formel
= 2(x2 – 6x + 9) +5 |ausmultiplizieren
=2x2 – 12x + 18 + 5 |zusammenfassen
=2x2 – 12x + 23
3.4. Schnittpunkte berechnen
Bei den quadratischen Funktionen kann man verschiedene Schnittpunktberechnungen machen. Zum einen kann man die Schnittpunkte zweier Parabeln und zum anderen die Schnittpunkte einer Parabel mit einer Geraden berechnen. Hierzu setzt man die beiden Funktionen gleich (f(x)=g(x)).
Beispiel:
Parabel f(x) = 2x2 – 12x – 16 und
Gerade g(x) = 4x + 2 | gleichsetzen
2x2 – 12x – 16 = 4x + 2 | Seiten tauschen und Zusammenfassen
2x2 – 16x -18 = 0 | Normalform erzeugen :2
x2 – 8x – 9 = 0 | p-q-Formel
x1/2 = 4 ±√(16+9) = 4 ± 5
x1 = 9; x2 = -1
y1 = 4‧9 + 2 = 38; y2 = 4‧(– 1) + 2= – 2
→ S1(9|38); S2(– 1|– 2)
Hat man bei dieser Berechnung nur eine Lösung, so berührt die Gerade die Parabel nur in einem Punkt. Dann nennt man diese Gerade eine Tangente der Parabel in diesem Berührpunkt.
3.5. Tangente Berechnen
- Der Punkt P liegt auf der Parabel
Möchte man eine Tangente in einem Punkt P(x1|y1) an die Parabel f(x)=ax2 berechnen, so muss man eine Gerade y = mx + b finden, die die Parabel nur in einem Punkt berührt, d.h. bei der Schnittpunktberechnung nur einen gemeinsamen Punkt hat.
ax2 = mx + b ↔ ax2 – mx – b = 0 ↔ x2 – (m/a)x – b/a = 0
x1/2 = (m/2a) ±√((-m/2a)2 +b/a)
Man hat nur eine Lösung, wenn die Wurzel Null ist,
also ist x1 = m/2a oder m = 2a•x1. Dies ist die Steigung der Tangente.
Die Berechnung von b der Tangente y = mx + b erfolgt mit Hilfe des Punktes P.
y1 = a(x1)2 ; Nun alles in die Tangente einsetzen ergibt:
a(x1)2 = 2a‧x1‧x1 + b↔ – a(x1)2 = b
Die Tangentengleichung lautet: y = 2a‧x1‧x – a(x1)2
- Der Punkt P liegt unterhalb oder oberhalb der Parabel
Möchte man eine Tangente von einem Punkt P(x1|y1) aus an die Parabel f(x)=ax2 berechnen, so ist die Berechnung vielkomplizierter, da man einen Punkt Q auf der Parabel finden muss, wobei auch hier die Parabel und die Tangente nur einen Berührpunkt haben darf.
Hier folgt ein Beispiel:
3.6. Parabel aus drei Punkten bestimmen
Hat man drei Punkte einer Parabel gegeben, so müssen beim Einsetzen der X-Werte bei der quadratischen Funktion die Y-Werte herauskommen. Aus jedem Punkt der Parabel erhält man eine Gleichung – insgesamt erhält man ein Gleichungssystem von drei Gleichungen mit 3 Variablen.


3.7. Übungsaufgaben
Aufgabe 1: Berechne zu folgenden Funktionen den Scheitelpunkt und die Nullstellen.
a) f(x) = x2 + 2x – 8 b) f(x) = x2 + 1/2x – 2
c) f(x) = x2 + 10x – 11 d) f(x) =x 2 + 2/3x + 1

Aufgabe 2: Bestimme folgende Normalparabeln.
- Der Scheitelpunkt liegt bei S1(-1|4) und ist nach oben geöffnet.
- Der Scheitelpunkt liegt bei S2(2|-3) und ist nach unten geöffnet.
- Die Normalparabel f(x) = x2 wird um 4 Einheiten nach rechts und um 3 Einheiten nach unten verschoben.
- Die Normalparabel f(x) = x2 wird um 3 Einheiten nach links verschoben und an der x-Achse gespiegelt.
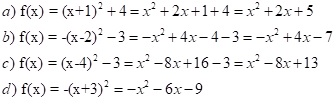
Aufgabe 3: Bestimme die Nullstellen von
- f(x) = x2 – 9
- f(x) = x2 + 6x
- f(x) = x2 + 2x – 8
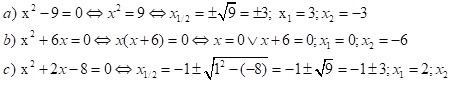
Aufgabe 4: Gegeben sind die Parabeln f(x) = 2x2 – 16x + 35 und g(x) = x2 + 2x – 21 und die Gerade h(x) = 2x – 3
- Berechne die Schnittpunkte der beiden Parabeln.
- Wo trifft die Gerade h die Parabel f(x) bzw. g(x)?
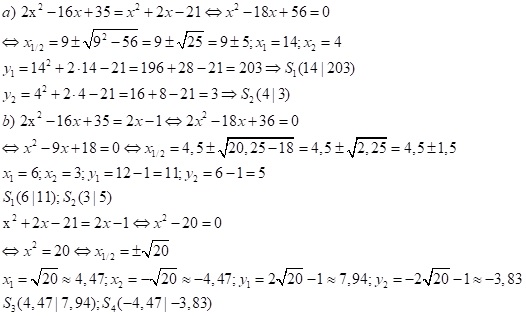
Aufgabe 5: Anwendungsaufgabe Gerade und Parabel
Der Teil eines Gebirges verläuft zwischen den Punkten A(2|2) und B(6|10) wie die Parabel mit der Funktionsgleichung y = x2 – 6x + 10. Zwischen den Punkten A und B soll ein Seil gespannt werden, um Lebensmittel von A nach B befördern zu können.
- Stelle eine Gleichung der Geraden auf, die durch die Punkte A und B verläuft.
- Wie lang muss das Verbindungsseil mindestens sein?
- Berechne den tiefsten Punkt des Tales, das mit dem Seil überspannt wird.
- Zur Unterstützung des Seiles soll im Mittelpunkt des Seiles eine Verankerung
am Berg senkrecht zum Seil angebracht werden. Stelle eine Geradengleichung
dieser Verankerung auf. Wo wird die Verankerung am Berg befestigt?
(Runde auf 2 Dezimalstellen)
Aufgabe 6: Bestimme die quadratische Funktion f, die durch die drei Punkte A, B und C verläuft.
- A(1/3) , B(-2/18) , C(4/24) Lösung: f(x) = 2x2 – 3x + 4
- A(2/-22) , B(1/-12) , C(-3/-52) Lösung: f(x) = -4x2 + 2x – 10
- A(2/-1,5) , B(-4/-10,5) , C(0/-6,5) Lösung: f(x) = 0,25x2 + 2x – 6,5
- A(2/0) , B(-1/9) , C(5/-63) Lösung: f(x) = -3x2 + 12
- A(2/ ) , B( /-1) , C(-3/44,5 ) Lösung: f(x) = 2x2 – 8x +2,5
Aufgabe 7:
Für einen Dokumentarfilm soll die Müngstener Brücke in einer Computersimulation zerstört werden. Als Vorlage steht das nebenstehende Luftbild zu Verfügung, indem schon einige Vermessungen eingetragen sind. Zur Realisierung der Computersimulation wird die Funktionsgleichung, die den Brückenverlauf darstellt, benötigt.
Lege ein Koordinatensystem in die Grafik und berechne damit die quadratische Funktion, die den unteren Brückenbogen beschreibt.

3.8. Klausuraufgaben
Aufgabe 1:
Gegeben sind die quadratischen Funktionen f(x) = x2 + 4x – 5, g(x) = 3x2 + x – 5
und h(x) = ½ x2 + 5
- Berechnen Sie die Scheitelpunkte von f(x) und h(x).
- Bestimmen Sie rechnerisch die Nullstellen von g(x).
- Ermitteln Sie rechnerisch die Schnittpunkte der beiden Funktionen f(x) und g(x)!
- Ferner ist die Funktion k mit k(x) = ax + 3, a ϵℝ gegeben. Bestimmen Sie den Parameter a so, dass h und k genau einen gemeinsamen Schnittpunkt besitzen.
Aufgabe2:
Von einem Berg soll Wasser mittels eines Grabens abgeleitet werden. Der Querschnitt dieses Grabens hat das untenstehende Profil. Dieses Profil ist durch einen Parabelbogen festgelegt, von dem die Punkte A(2|-1), B(-2|7) und C(5|14) bekannt sind.
a) Bestimmen Sie die Funktionsgleichung der Parabel f.
Der Graph, der durch die Punkte A, B und C verläuft, hat die Funktionsgleichung
f(x) = x2 – 2x – 1.
Über diesen Graben soll eine Brücke gebaut werden. Dazu muss die Breite des Grabens bekannt sein. In der Nähe des Grabens kann der Berg durch die Gerade mit g(x) = – x + 2,75 beschrieben werden.
b) Bestimmen Sie die Schnittpunkte der Geraden g mit der Parabel f. Berechnen Sie auch die Breite des Grabens, indem Sie den Abstand zwischen den Schnittpunkten bestimmen.
c) Bei dem Bau des Grabens stellt man fest, dass sich in einer bestimmten Tiefe eine undurchdringliche Gesteinsschicht befindet. Diese Schicht beginnt direkt unterhalb der X-Achse. Es wird ein neuer Graben geplant, der diese Schicht (= x-Achse) nicht berührt und auch nicht schneidet. Das Profil des neu geplanten Grabens lässt sich durch die Funktionsgleichung f(x) = x2 – 2x + c beschreiben.
Untersuchen Sie wie der Parameter c gewählt werden muss, damit der neue Graben die Vorgaben erfüllt!
