Lineare Funktionen

 

2.  Lineare Funktionen  – Geraden

2.1. Beschreibung linearer Funktionen

Zusammenhänge, die sich ganz gleichmäßig (proportional) verhalten, lassen sich in ein Koordinatensystem eintragen und ergeben eine lineare Funktion – eine Gerade.

Eine Funktion, deren Funktionsgleichung  man als y = m•x+b   schreiben kann, heißt lineare Funktion.  (m ist die Steigung, b ist der y-Achsenabschnitt der Geraden)
z.B. y = 2x + 3
Die Geradengleichung nennt man Normalform oder Hauptform der Geradengleichung.

  • Will man wissen, ob ein Punkt auf einer gegebenen Funktion liegt, so macht man einfach eine Punktprobe, d.h. man setzt die Koordinaten des Punktes in die Funktionsgleichung ein und prüft, ob sie die Gleichung erfüllen.

Beispiel:

Liegt der Punkt P (1,5 | 3) auf dem Graphen der Funktion y = 2x +3?

Punktprobe:   3 = 2•1,5 + 3
                        3 ≠ 6

Also liegt der Punkt nicht auf dem Schaubild der Funktion f.

2.2. Steigung von Geraden, orthogonale Geraden

Betrachtet man das Steigungsdreieck, so
erkennt man die Steigung m der Geraden,
die durch die Punkte P und Q geht:
        YQ – YP
m = ————    (wobei XQ – XP ≠ 0)
        XQ – XP

 Für den Steigungswinkel α gilt:
tan(α) = m     (mit 0° < α < 180°)

                                 Gegenkathete
(weil der Tangens = ——————–  ist)
                                    Ankathete

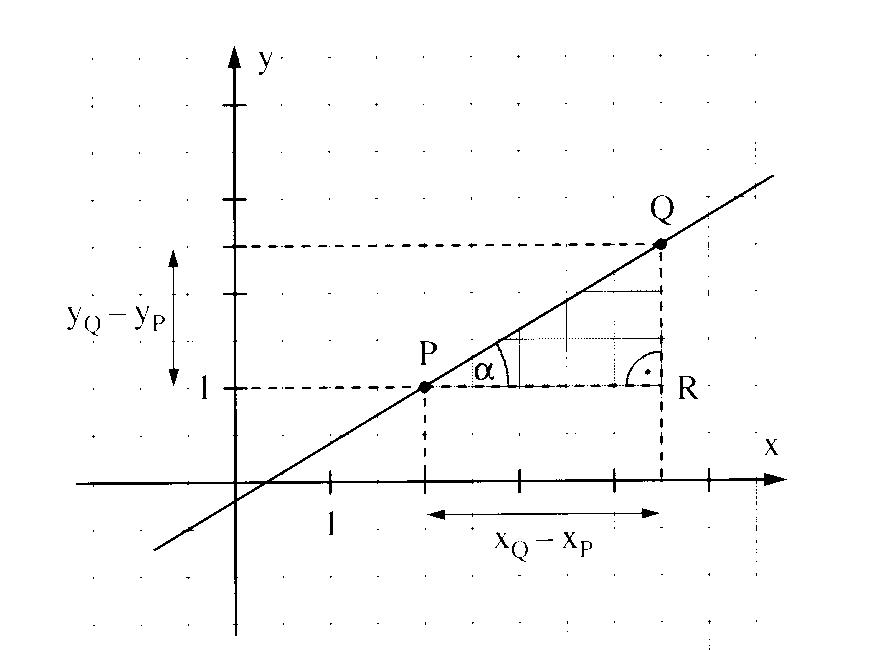
Beispiel:

Für obige Gerade gilt: m = (2,5 – 1)/(4,5 – 2) = 1,5/2,5 = 3/5 = 0,6  und damit α ≈30,96° 
(TR: SHIFT TAN 0,6)

Bemerkung:

Betrachten wir eine Gerade, die senkrecht (= orthogonal) zur obigen ist, so fällt diese (d.h. negative Steigung), x und y vertauschen sich, d.h.  nach dem Steigungsdreieck ist dann: m = -5/3 ≈ -1,67

Wir betrachten zwei Geraden mit den Steigungen m1 und m2: Allgemein gilt:
1. Wenn die beiden Geraden orthogonal sind, so gilt:m2 = – 1/m1  (oder m1 • m2 = -1)
2. Und umgekehrt: Gilt m1 • m2 = -1, so sind die beiden Geraden orthogonal.

2.3. Berechnung einer Geradengleichung
Fall 1: (Die Steigung m und ein beliebiger Punkt P der Geraden ist bekannt)

Was macht man aber, wenn von der Geraden nur die Steigung m und ein beliebiger Punkt P (xp | yp) bekannt ist?

Beispiel:

Gegeben: m=3/5=0,6, P (2 | 1)
Setze m, xp, yp in die Normalform ein und löse nach b auf.

1 = 3/5•2 + b ↔1 – 1,2 = b↔b = – 0,2= – 1/5

→y = 0,6 x -0,2 oder y = 3/5 x -1/5

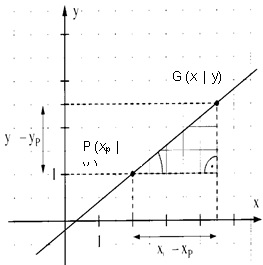
Macht man dies allgemein für einen bel. Punkt, so erhält

man die Punktsteigungsform. 

Dann gilt für jeden Punkt G (x | y) der Geraden
die Punktsteigungsform    m = (y – yp)/(x – xp) 

Durch Umformung erhält man folgende Formeln:

m(x – xp)=(y – yp) oder mx – mxp + yp = y

Fall 2: (Zwei beliebige Punkte P und Q der Geraden seien bekannt)

Und was macht man, wenn von der Geraden lediglich zwei Punkte P und Q bekannt sind? Dann kann man die Steigung m aus den zwei Punkten P und Q nach m = (yq – yp)/(xq – xp)  berechnen und b wie in Fall 1 berechnen.

Beispiel:

Gegeben: P (2 | 1)  und   Q (4,5 | 2,5)

Berechnung von m: m = (yq – yp)/(xq – xp) = (2,5 – 1)/(4,5 – 2)=1,5/2,5 = 3/5 = 0,6

Setze m, xp, yp  in die Normalform ein und löse nach b auf.

1 = 3/5•2 + b ↔b = -1/5 → y = 3/5•x – 1/5

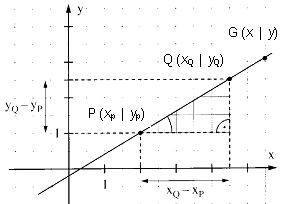
Macht man diese Rechnung allgemein mit Variablen, so erhält man eine Formel – die Zweipunkteform.

Für jeden Punkt G (x | y) der Geraden gilt
die Zweipunkteform (y – yp)/(x – xp) = (yq – yp)/(xq – xp)

Stellt man diese Gleichung um, so erhält man folgende Formeln:

(y – yp)= (yq – yp) (x – xp) /(xq – xp)

(y – yp)= (yq – yp) /(xq – xp)  x – (yq – yp) /(xq – xp)   xp

y  = (yq – yp) /(xq – xp)  x – (yq – yp) /(xq – xp)   xp + yp

2.4. Schnittpunkt zweier Geraden

Den Schnittpunkt zweier Geraden erhält man, indem man die Geradengleichungen gleichsetzt (y entfällt somit) und die Gleichung nach x auflöst. Den y-Wert des Schnittpunktes erhält man dann durch einsetzen in eine der beiden Geradengleichungen.

Beispiel: (1) y = 2x  + 1    (2) y = 4x – 3

2x + 1 = 4x – 3 ↔-2x = -4 ↔ x = 2

y = 2•2 + 1 = 5 → S(2 |5)

2.5. Länge und Mittelpunkt einer Strecke

Die Länge  der Strecke PQ
lässt sich nach dem Satz des Pythagoras berechnen:
(Stell dir ein rechtwinkliges Dreieck vor)
|PQ| = √(xq – xp)2 + (yq – xp)2

Mittelpunkt M(xm | ym) einer Strecke PQ:
Um dessen Koordinaten zu berechnen, bilde das arithmetische Mittel aus xp und xq  
(bzw. aus yp und yq).     – vgl. Notendurchschnitt: alles zusammenzählen und durch n teilen.
xm = ½ (xp + xq) und ym = ½ (yp + yq)     M (½ (xp + xq) | ½ (yp + yq))

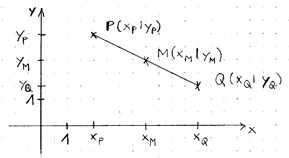
Beispiel:

In obigem Schaubild ist P (2 | 3,5) und Q (6 | 1,5).

  1. Die Länge der Strecke PQ ist:  |PQ| = √((6 – 2)2 + (1,5 – 3,5)2 )=√(42 +(-2)2 )= √(16 + 4) =√20 = 2√5 ≈ 4,47 LE    
  1. Die Koordinaten des Mittelpunkts der Strecke PQ sind:
    xm = ½ (2+6) = 4 ym = ½ (3,5 + 1,5) = 2,5 also ist M (4 | 2,5).

2.6. Aufgaben zu linearen Funktionen

Aufgabe 1: Berechne eine Geradengleichung für g, die durch den Punkt P(2 |-5) verläuft und die Steigung m = 3 hat. Welche Gerade h verläuft senkrecht zu g in diesem Punkt P?

Aufgabe 2:  Berechne eine Geradengleichung für g, die durch die Punkte P(-1 |3) und Q(3 |-2) verläuft. Liegt der Punkt A(-4 |6) auch auf dieser Geraden g?

Aufgabe 3: Gegeben sind die Punkte A(2 |6) und B(-3 |-4). Berechne die Länge der Strecke zwischen A und B. Welche Koordinaten hat der Mttelpunkt zwischen A und B?

Aufgabe 4: Gegeben ist das Dreieck ABC mit A(-1 |3), B(4 |1) und C(2 |7).

  1. Berechne eine Gerade g parallel zur Seite c durch den Eckpunkt C.
  2. Berechne eine orthogonale Gerade h zur Seite c durch den Eckpunkt B.
  3. Bestimme den Schnittpunkt dieser neuen Geraden g und h.

Aufgabe 5: Gegeben sind die Geraden g mit y = 3x + 1 und h mit y = -2x – 3.

  1. Überprüfe, ob der Punkt P(2 |-3) auf der Geraden g oder h liegt.
  2. Berechne den Schnittpunkt der beiden Geraden g und h.

Aufgabe 6: Gegeben ist das Dreieck ABC mit A(-3 |-4), B(5 |-2) und C(1 |4).

  1. Berechne die Mittelpunkte und die Steigungen der Seiten a, b und c.
  2. Berechne die Geraden der Seitenhalbierenden des Dreiecks ABC und zeige, dass sie sich in einem Punkt schneiden.
  3. Berechne die Geraden der Mittelsenkrechten des Dreiecks ABC und zeige, dass sie sich in einem Punkt schneiden.
  4. Berechne die Geraden der Höhengeraden des Dreiecks ABC und zeige, dass sie sich in einem Punkt schneiden.
  5. Bestimme den Umfang des Dreiecks ABC.
  6. Berechne einen Eckpunkt D so, dass das Viereck ABDC ein Parallelogramm ergibt.

Aufgabe 1: Berechne eine Geradengleichung für g, die durch den Punkt P(2 |-5) verläuft und die Steigung m = 3 hat. Welche Gerade h verläuft senkrecht zu g in diesem Punkt P?

y = 3\cdot x +b\\ -5 = 3\cdot 2 + b\\ b = -11, d.h. y = 3\cdot x - 11\\ \\ Senkrechte Gerade: m = -\frac{1}{3}\\ \\ y = -\frac{1}{3}\cdot x +b\\ -5 = -\frac{1}{3}\cdot 2 + b\\ b = -\frac{13}{3}, d.h. y = -\frac{1}{3}\cdot x -\frac{13}{3}

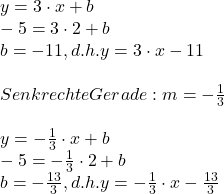
Aufgabe 2:  Berechne eine Geradengleichung für g, die durch die Punkte P(-1 |3) und Q(3 |-2) verläuft. Liegt der Punkt A(-4 |6) auch auf dieser Geraden g?

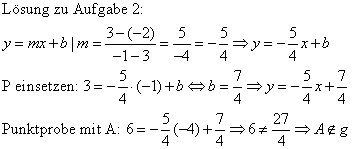
Aufgabe 3: Gegeben sind die Punkte A(2 |6) und B(-3 |-4). Berechne die Länge der Strecke zwischen A und B. Welche Koordinaten hat der Mittelpunkt zwischen A und B?

 

Aufgabe 4: Gegeben ist das Dreieck ABC mit A(-1 |3), B(4 |1) und C(2 |7).

 

  1. Berechne eine Gerade g parallel zur Seite c durch den Eckpunkt C.
  2. Berechne eine orthogonale Gerade h zur Seite c durch den Eckpunkt B.
  3. Bestimme den Schnittpunkt dieser neuen Geraden g und h.

Aufgabe 5: Gegeben sind die Geraden g mit y = 3x + 1 und h mit y = -2x – 3.

 

  1. Überprüfe, ob der Punkt P(2 |-3) auf der Geraden g oder h liegt.
  2. Berechne den Schnittpunkt der beiden Geraden g und h.

Aufgabe 6: Gegeben ist das Dreieck ABC mit A(-3 |-4), B(5 |-2) und C(1 |4).

 

  1. Berechne die Mittelpunkte und die Steigungen der Seiten a, b und c.
  2. Berechne die Geraden der Seitenhalbierenden des Dreiecks ABC und zeige, dass sie sich in einem Punkt schneiden.
  3. Berechne die Geraden der Mittelsenkrechten des Dreiecks ABC und zeige, dass sie sich in einem Punkt schneiden.
  4. Berechne die Geraden der Höhengeraden des Dreiecks ABC und zeige, dass sie sich in einem Punkt schneiden.
  5. Bestimme den Umfang des Dreiecks ABC.
  6. Berechne einen Eckpunkt D so, dass das Viereck ABDC ein Parallelogramm ergibt.

2.7. Klausuraufgaben

 

Aufgabe 1: Die Gerade g hat die Steigung m = -3/2und geht durch den Punkt P (-2 | 6).

Die Gerade h verläuft durch die Punkte A (-9 | -6,5) und B (1 | -1,5).

  1. Bestimme die Funktionsgleichungen der zugehörigen linearen Funktionen.
  2. Zeichne die beiden Geraden in ein
  3. Bestimme rechnerisch für beide Geraden die Nullstellen.
  4. Die beiden Geraden schneiden sich in einem Punkt S. Berechne die Koordinaten des Schnittpunktes.
  5. Gib die Gleichung einer Geraden k an, die durch den Koordinatenursprung geht und parallel zu der Geraden g ist.
  6. Gesucht ist eine Geraden t, die durch den Punkt T (-15 | 18) geht und orthogonal zu der Geraden g verläuft.

Aufgabe 2:

Die Punkte A (-4 | 3) , B ( -2 | -3) und C (1 | 2) sind Eckpunkte eines Dreiecks.

  1. Zeichne das Dreieck in ein Koordinatensystem
  2. Bestimme rechnerisch den Umfang des Dreiecks.
  3. Bestimme rechnerisch die Gleichung der Seitenhalbierenden s c auf die Dreiecksseite AB.
  4. Ermittle die Mittelsenkrechte m a auf die Dreiecksseite BC.

Aufgabe 3:

Ein Segelflugzeug verliert pro Minute 50m Höhe, bei einer Geschwindigkeit von 70km/h ohne störende Auf- und Abwinde. Der Pilot setzt in einer Höhe von 2500m über dem Erdboden zum Gleitflug an.

  1. Zeichne den Graphen der Funktion Zeit t (in min) Höhe h (in m).
  2. Der Graph dieser Funktion ist eine Gerade. Gib für diese Gerade eine Funktionsgleichung an.
  3. Mit welcher Höhe kann der Pilot nach 10 Minuten noch rechnen?
  4. Nach welcher Flugzeit erreicht das Segelflugzeug voraussichtlich den Erdboden?

Aufgabe 4: Die Funktion f hat den Term y = √x+3 

  1. Berechne f(-2), f(-1,5), f(0), f(1), f(a) und f(a2-3).
  2. Gib den maximalen Definitionsbereich und Wertebereich von f an.
  3. Zeichne den Graphen von f über dem Intervall von -4 bis +4.
  4. Prüfe, ob die Punkte P1(1 |3) und P2(6 |3) auf dem Funktionsgraphen von f liegen.

 

Aufgabe 5: Gegeben sind die Geraden g1: y = 3/2 x + 2 und g2: y = 2x – 3/4

  1. Zeichne die Geraden g1 und g2 in ein Koordinatensystem.
  2. Bestimme rechnerisch den Schnittpunkt von g1 und g2.
  3. Gib zu der Geraden g1 eine parallele Gerade und zur Geraden g2 eine orthogonale Gerade an, die durch den Punkt P(2 |3) verlaufen.

 

Aufgabe 6: Gegeben ist das Dreieck ABC mit A(-4 |3), B(-2 |-3) und C(1 |2).

  1. Zeichne das Dreieck in ein Koordinatensystem.
  2. Bestimme die Gleichungen der Seitengeraden.
  3. Berechne den Umfang des Dreiecks.
  4. Berechne die Mittelsenkrechten der Seiten und zeige, dass die Mittelsenkrechten sich in einem Punkt schneiden.

Aufgabe 7:     Gegeben sind die Punkte P1(2|5) und P2(6|7).

  1. Stellen Sie die Funktionsgleichung der Geraden g durch die Punkte P1 und P2
  2. Die Schnittpunkte der Geraden g mit den Koordinatenachsen bilden gemeinsam mit dem Koordinatenursprung ein rechtwinkliges Dreieck. Berechnen Sie den Flächeninhalt des Dreiecks.

Aufgabe 8:     Gegeben sind die Geraden g und h mit den Funktionsgleichungen

g(x) = 1/4x + 1 und h(x) = 2x + 8

  1. Bestimmen Sie den Schnittpunkt der beiden Geraden g und h.
  2. Bestimmen Sie zur Geraden h eine parallele Gerade, die durch den Koordinatenursprung geht.
  3. Bestimmen Sie zur Geraden h eine senkrechte Gerade durch den Punkt B(-2|4).
    Hinweis: Zwei Geraden sind senkrecht, wenn für die Steigungen gilt: m2 = – 1/m2

Aufgabe 9:     Gegeben sind die Punkte A(5|-1), B(9|1) und C(7|5).

  1. Zeigen Sie rechnerisch, dass die Punkte A, B und C ein Dreieck aufspannen.
  2. Berechnen Sie den Umfang des Dreiecks ABC.
  3. Berechnen Sie die Mittelpunkte der Seiten des Dreiecks ABC.
  4. Bestimme eine Geradengleichung für die Seitenhalbierende zur Seite a.

 

Aufgabe 10:  Ein Fallschirmspringer öffnet seinen Fallschirm und misst  zu verschiedenen Zeitpunkten nach dem Öffnen des Schirms die Höhe über dem Erdboden. Die Messung ergab folgende Wertetabelle.

          

  1. Begründen Sie, warum der Zusammenhang zwischen der Fallzeit t und der Höhe h im gemessenen Intervall durch eine lineare Funktion beschrieben werden kann.
  2. Bestimmen Sie die Steigung dieser linearen Funktion und erklären Sie die Bedeutung dieses Wertes im Sachzusammenhang.
  3. Geben Sie den Funktionsterm dieser linearen Funktion an und erklären Sie die Bedeutung des y-Achsenabschnittes im Sachzusammenhang.
  4. Berechnen Sie die Höhe des Fallschirmspringers nach 33 Sekunden.
  5. Berechnen Sie den Zeitpunkt, zu dem der Fallschirmspringer eine Höhe von 100m erreicht hat.
  6. Berechnen Sie den Zeitpunkt der Landung auf dem Erdboden.